


- 首页
- 产品
- 下载
-
帮助中心
SPSS三因素方差分析举例 SPSS三因素方差分析步骤
发布时间:2022-05-19 14: 30: 16
品牌型号:联想GeekPro 2020
系统: Windows 10 64位专业版
软件版本: IBM SPSS Statistics
SPSS三因素方差分析举例,三因素方差分析是一种多因素方差分析,常用于分析多个自变量对因变量产生的影响,当包含三个自变量时,即为三因素方差分析,本文会举例说明,同时会演示SPSS三因素方差分析步骤。
一、SPSS三因素方差分析举例
SPSS三因素方差分析,即包含三个自变量的多因素方差分析,常用于研究多个自变量对单个因变量产生的影响,比如研究影响种子发芽率的因素,影响顾客满意度的因素,影响工资的因素等,都可以使用多因素方差分析,如果影响因素为三个变量的话,就构成了spss的三因素方差分析。
本文会举例研究影响工资的三个因素:工作年限、区域、城市,来进一步演示spss三因素方差分析的方法。
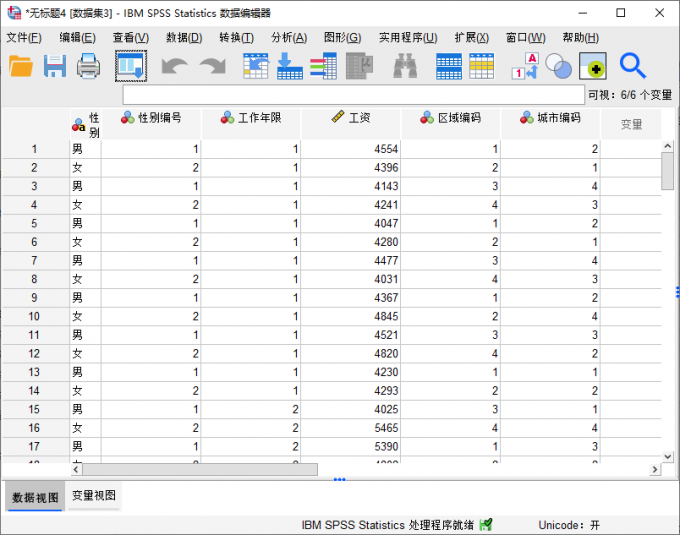
图1:示例数据 二、SPSS三因素方差分析步骤
接下来,我们应用上述数据演示spss三因素方差分析步骤如下:
第一步、选择分析方法
依次单击spss分析-一般线性模型-单变量选项。这里需要注意的是,虽然spss三因素方差分析引入了三个变量,但都是自变量,因此使用的是单变量分析,多变量分析是用于多个因变量的情况。
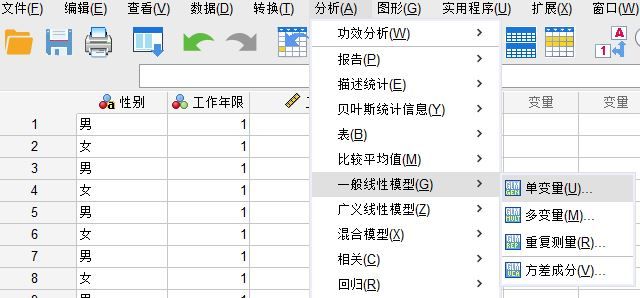
图2:单变量分析方法 第二步、选择变量
为三因素方差分析设置变量,主要包括因变量与固定因子的设置。
1. 因变量,多因素方差分析只能选择一个因变量,即研究多因素影响是否显著的变量,本例将“工资”作为因变量,以研究多因素对工资产生的影响是否显著。
2. 固定因子,即影响的因素,三因素方差分析选择三个固定因子,本例将“工作年限”、“区域编码”、“城市编码”设置为固定因子。需要注意将名义变量转换为数值变量,比如区域、城市需提前转换成编码,如果是字符串将无法运算。
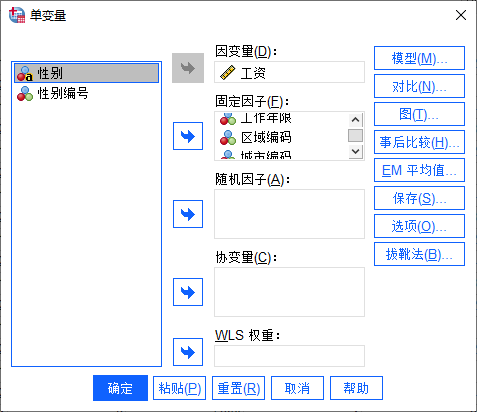
图3:选择变量 第三步、设置统计量
“估计边际平均值”可用于检验因子之间的交互显著性,选择“overall”可包含主效应与交互效应的分析,即“因子与因子交互”列表中所有项目的效应分析,可检验不同因素,以及不同因素交互后对因变量是否有显著影响。
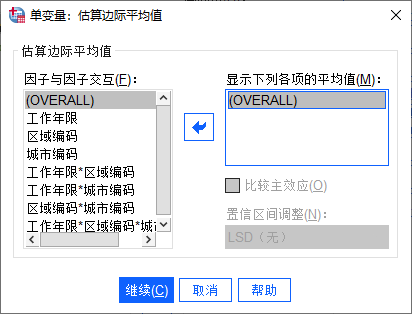
图4:估算边际平均值 “齐性检验”,检验事后多重分析(分析自变量的数值间是否有显著性差异)是否满足等方差的假设,对于显著性水平,一般保持0.05即可。
“描述统计”,运算均值、方差等统计数值,以了解数据的分布与离散程度。。
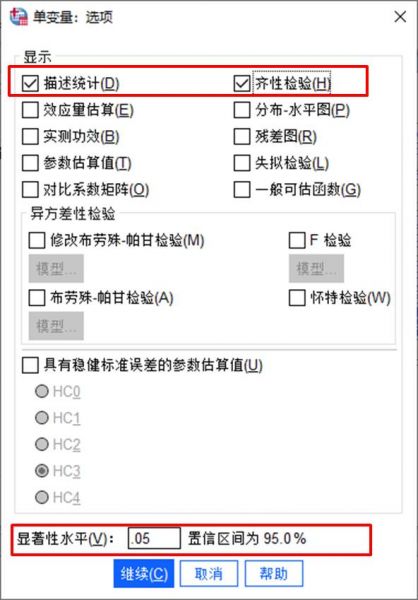
图5:选项设置 在进行三因素方差分析时,除了分析不同因素对因变量产生的影响外,还可通过“事后多重比较”,进行自变量数值对因变量的影响差异性检验。我们可以将“工作年限”、“区域编码”、“城市编码”添加到事后检验,用于检验不同工作年限、不同区域、不同城市对工资产生差异影响的显著性。
如果满足“齐性检验”中的等方差假设,可选用“LSD法”,也就是最小显著性差异法,因其检验敏锐度比较好,SNK检验虽然与LSD检验相似,但检验结果更为保守,比较适用于两两比较。
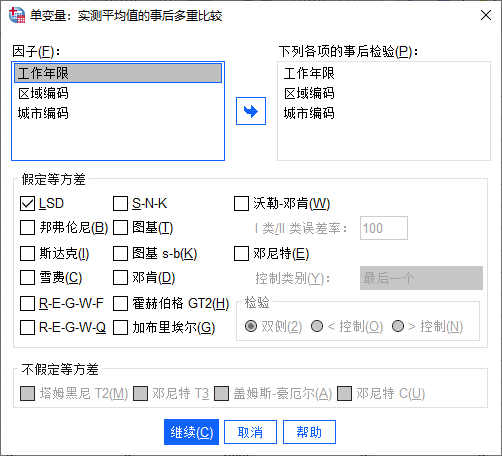
图6:事后多重比较设置 三、SPSS三因素方差分析结果解读
完成以上设置,运行SPSS的三因素方差分析并解读结果。
首先看到,本例使用了三个主体间因子,分别是“工作年限”、“区域”与“城市”,其样本量如图7所示
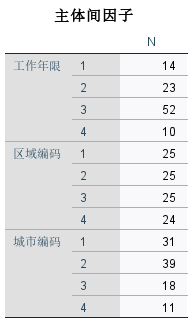
图7:样本分布 接着,查看主体间的效应检验结果。
先看“工作年限”、“区域”与“城市”三个因素的显著性,其中“工作年限”显著性<0.001,影响显著,而“区域”与“城市”显著性均大于>0.05,影响不显著。
另外,“工作年限*区域”的协同影响显著性为0.039<0.05,协同影响显著,但推断更多来自于“工作年限”的影响。
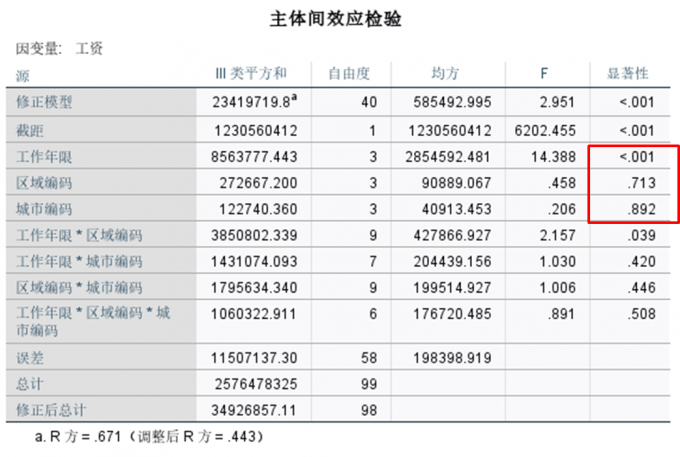
图8:主体间效应检验 在知道“工作年限”对“工资”有显著影响后,我们可能还会想知道哪些年限之间有显著的影响差异,鉴于此,需要进一步查看“事后多重比较”结果。
由于“事后多重比较检验”在使用LSD(最小显著性差异法)检验时,需确保数据满足方差齐性的假设,因此,需先查看“方差齐性检验”结果。
如图9所示,“基于平均值”的方差齐性显著性数值为0.062>0.05,检验结果不显著,不能拒绝原假设,也就是满足方差齐性假设。
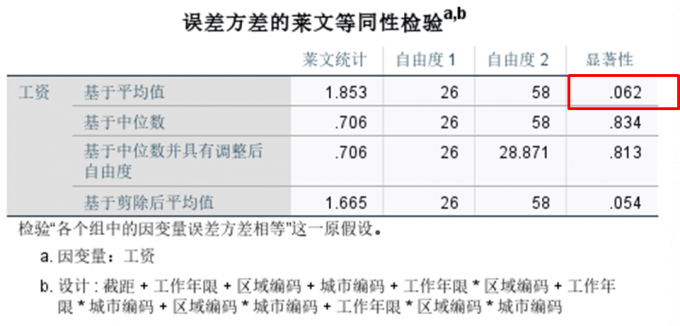
图9:方差齐性检验 在满足方差齐性的前提下,查看“工作年限”的LSD多重比较数据。
从显著性数值(均小于0.05)看到,不同工作年限的工资数值都有显著性差异,工作年限越长与工作年限越短的差异更为明显。

图10:多重比较(工作年限) 四、小结
以上就是关于SPSS三因素方差分析举例,SPSS三因素方差分析步骤的相关内容。SPSS三因素方差分析是包含三个自变量的多因素方差分析,操作的时候,注意要与多变量方差分析区分开来,另外,三因素方差分析可通过事后多项比较检验自变量数值间的影响差异的显著性。
作者:泽洋
展开阅读全文
︾
标签:多因素方差分析,协方差分析,多元方差分析,方差分析,方差齐性检验
读者也访问过这里:热门文章SPSS数据分析显著性差异分析步骤 SPSS显著性差异分析结果怎么看数据的显著性差异分析主要有三种方法,分别是卡方检验、T检验和方差分析。这三种方法都有具体的数据要求:卡方检验是对多个类别的数据进行分析,T检验是对两组数据进行分析,方差分析是对多组数据进行检验。下面,小编具体说明一下SPSS数据分析显著性差异分析步骤,SPSS显著性差异分析结果怎么看。2022-01-07实践SPSS单因素方差分析之检验结果解读在《实践SPSS单因素方差分析之变量与检验方法设置》一文中,我们已经详细地演示了IBM SPSS Statistics单因素方差分析方法的变量选择以及相关的选项、对比设置。2021-01-11spss如何做显著性分析 spss显著性差异分析怎么标abc在统计分析中,显著性分析是分析相关因素之间是否存在显著影响关系的关键性指标,通过它可以说明分析结论是否由抽样误差引起还是实际相关的,可论证分析结果的准确性。下面大家一起来看看用spss如何做显著性分析,spss显著性差异分析怎么标abc。2022-03-14SPSS回归分析中的f值是什么 SPSS回归分析F值在什么范围合适回归分析中以R表示相关性程度的高低,以F评价回归分析是否有统计学的意义,使用IBM SPSS Statistics进行回归分析,可以非常快速的完成R,F的计算,并且给出回归曲线方程,那么,SPSS回归分析中f值是什么?SPSS回归分析F值在什么范围合适,本文结合实例向大家作简单的说明。2022-07-22SPSS多元logistic回归分析的使用技巧回归分析是数据处理中较为常用的一类方法,它可以找出数据变量之间的未知关系,得到较为符合变量关系的数学表达式,以帮助用户完成数据分析。2021-04-26SPSS相关性分析结果怎么看相关性分析是对变量或个案之间相关度的测量,在SPSS中可以选择三种方法来进行相关性分析:双变量、偏相关和距离。2021-04-23最新文章SPSS折线图横坐标方向怎么调整 SPSS折线图横坐标不是变量怎么办在日常的数据分析工作中,我们可以根据折线图里的点位变化,清晰地看出数据的发展趋势,并将这些已有的趋势转化为未来的发展策略。今天我就以SPSS折线图横坐标方向怎么调整,SPSS折线图横坐标不是变量怎么办这两个问题为例,来向大家讲解一下SPSS中调节折线图横坐标的相关操作技巧。2026-03-03SPSS多个自变量拟合怎么做 SPSS多个自变量相关性检验怎么做用过IBM SPSS Statistics软件的用户应该都清楚它的强大,我们可以用它来进行复杂数据分析,比如多个自变量拟合、相关性检验分析等等,而且软件界面相当友好,刚接触的小白也能快速掌握,本期我们就来介绍一下SPSS多个自变量拟合怎么做,SPSS多个自变量相关性检验怎么做的相关内容。2026-01-30SPSS做ks和sw正态性检验步骤 SPSS正态性检验ks和sw怎么看说到IBM SPSS Statistics,大家第一时间想到的可能就是它的专业统计功能。SPSS软件的数据处理与分析功能确实非常不错,很多科研、教育、市场研究等领域的用户都在使用。不过很多新手可能会觉得操作步骤复杂,其实不然。接下来我们就来带大家了解一下SPSS做ks和sw正态性检验步骤,SPSS正态性检验ks和sw怎么看的相关内容。2026-01-30SPSS非参数检验怎么测中位数 SPSS非参数检验z值的意义IBM SPSS Statistics这款软件对用户非常友好,例如非参数检验、数据随机性验证等统计分析,不需要复杂的操作,跟着步骤提示进行操作,即可快速生成统计结果表,新手也能快速掌握。今天我们就围绕SPSS非参数检验怎么测中位数,SPSS非参数检验z值的意义相关内容为大家展开介绍。2026-01-30SPSS随机值检验步骤 SPSS随机检验结果怎么看很多人都听过IBM SPSS Statistics这款软件,它是数据分析的可靠搭档,不仅能轻松搞定数据的整理、转换,最后还能自动生成图表,对新手非常友好。对于经常需要进行学术研究、市场调研的用户来说是个常用的选择。今天我们就来说一下SPSS随机值检验步骤,SPSS随机检验结果怎么看的相关内容。2026-01-30SPSS为什么没有事后检验 SPSS事后检验结果怎么看SPSS作为一款优秀的数据统计分析软件,深受数据统计分析人员的喜爱。SPSS之所以这么受欢迎,除了SPSS有很多的数据统计分析方法,可以帮助统计分析人员更高效的进行数据分析,还因为SPSS的人性化操作,一些刚入行的统计小白,也可以快速的掌握SPSS,接下来给大家详细介绍有关SPSS为什么没有事后检验,SPSS事后检验结果怎么看的相关内容。2026-01-30微信公众号
欢迎加入 SPSS 产品的大家庭,立即扫码关注,获取更多软件动态和资源福利。
读者也喜欢这些内容:
-
SPSS显著性小于0.001的意义 SPSS显著性大于0.05怎么办
在使用SPSS软件进行数据分析工作的过程中,得到的显著性水平分析结果具有极为重要的作用。它能够帮助我们衡量变量之间是否存在真实的关联,或者不同组别数据之间是否存在实质性的差异。今天我们就一起来探讨关于SPSS显著性小于0.001的意义,SPSS显著性大于0.05怎么办的问题。...
阅读全文 >
-

SPSS汽车零部件行业应用案例
...
阅读全文 >
-

SPSS数字和字符串的区别 SPSS数字和数值一样吗
常规意义上我们理解的数据,可能只是各式各样的数字,但实际情况下,数值、文字、比值、区间等等,都囊括在数据分析工作的范围之内。今天我就以SPSS数字和字符串的区别,SPSS数据和数值一样吗这两个问题为例,来向大家讲解一下SPSS中不同变量类型之间的差别。...
阅读全文 >
-
SPSS将连续变量分成三类怎么做 SPSS将连续变量转换成类型变量怎么操作
连续变量是我们在数据分析工作中较为常见的数据类型,不同的连续变量共同构成了数据的底层基础。今天我就以SPSS将连续变量分成三类怎么做,SPSS将连续变量转换成类型变量怎么操作这两个问题为例,来向大家讲解一下连续变量的相关知识。...
阅读全文 >
-



