


- 首页
- 产品
- 下载
-
帮助中心
SPSS方差分析模型的参数估计 SPSS方差分析模型中两个变量合并
发布时间:2022-04-27 20: 00: 47
品牌型号:微星 gl62m
系统:Windows 11
软件版本:IBM SPSS Statistics
参数估计是统计推断的一种。根据从总体中抽取的随机样本来估计总体分布中未知参数的过程。在IBM SPSS Statistics里分析完一堆数据后,参数估计能给人带来最直观的模型概念,本文就来说说SPSS方差分析模型的参数估计,SPSS方差分析模型中两个变量合并的相关问题。
- 一、IBM SPSS Statistics方差分析模型的参数估计
IBM SPSS Statistics的参数估计方法也是在方差模型中的一部分,在方差分析的过程中只要添加一些选项就可以在结果中输出参数估计的结果,不过本文还是从头开始讲述如何做方差分析模型的参数估计。
1.导入数据
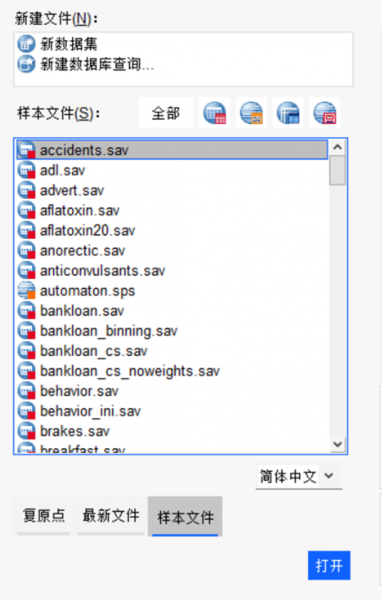
图1:导入数据 2.按顺序点击:分析——一般线性模型——多变量
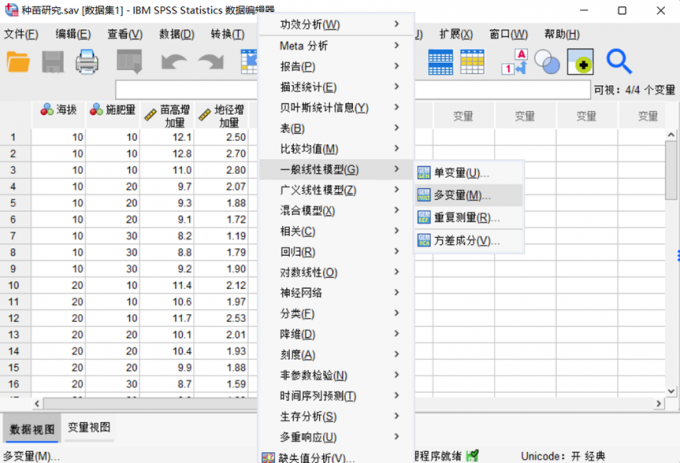
图2:变量线性模型选择 3.输入固定因子(控制变量)和因变量(观测变量)
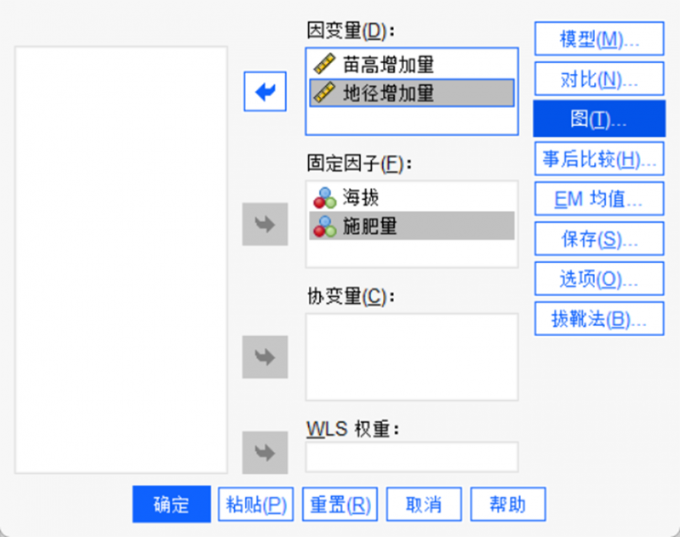
图3:填入变量页面 4.点击“事后比较”选项,在假定方差齐性区域选择,勾选“LSD”和“snk” 作为事后多重检验的检验方式
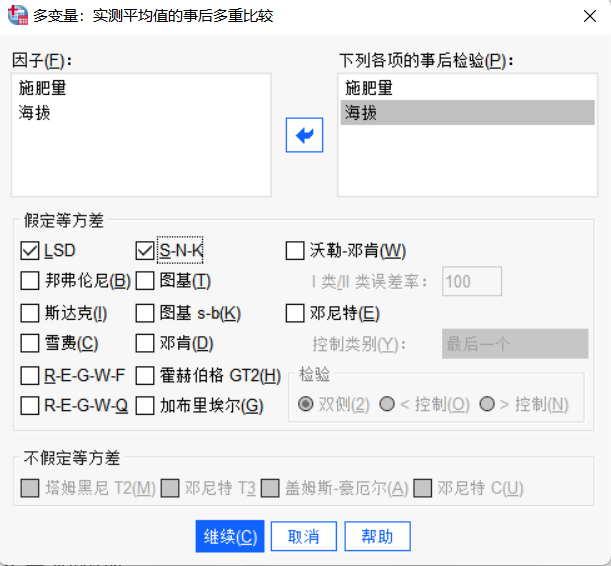
图4:事后检验 5.点击“选项”里,在显示区域选择描述统计、同质性检验、参数估计和对比系数矩阵。

图5:选项选择页面 6.返回,点击确定即可输出分析结果。
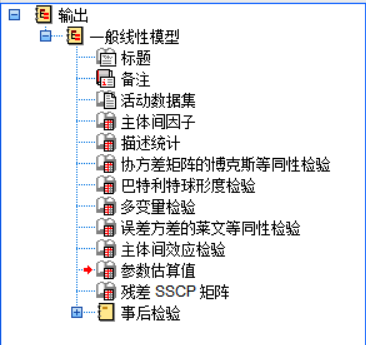
图6:输出结果 7.点击参数估算值,即为本文需要的方差分析模型的参数估计。
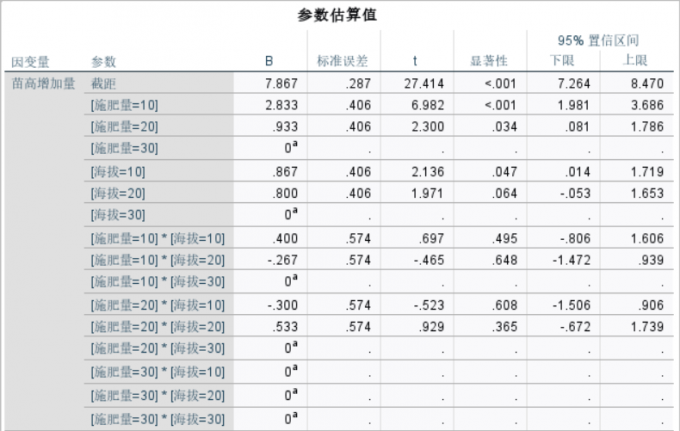
图7:参数估计1 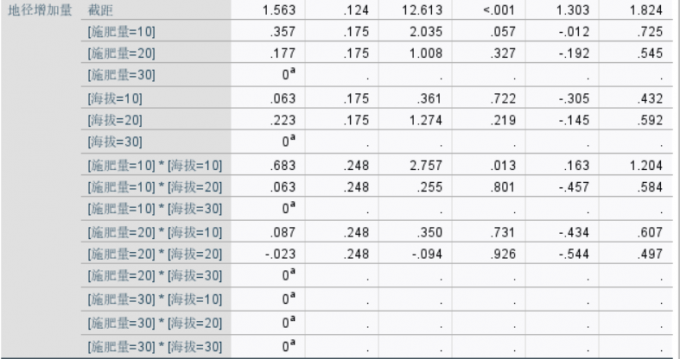
图8:参数估计2 上面两张表就是模型两个因变量各参数的估计值,截距就是不同施肥量、海拔以及其混合的水平,估计值分别为7.867和1.563,表示不考虑施肥量和海拔时,苗高增加量为7.867,地径增加量为1.563。从第二行开始就是对不同施肥量、海拔以及其混合的水平的估计,由于这些参数之间存在数量上的关联,必须要加上一定的限制条件才能进行估计,在本例中,模型默认将编号取值最高的施肥量30和海拔30作为参照水平,这相当于强迫a3=0,另外几组参数的估计值和检验结果实际上就等于与这两组进行对比的结果。
二、SPSS方差分析模型中两个变量合并
在存在多个数据源的情况下,经常会使用到IBM SPSS Statistics的变量合并功能,对多个数据源的数据进行合并。
- 1.打开需合并的数据其中一个(若两个要合并的数据文件不是按照记录编号的对应规则进行合并,则至少要有一个相同名称的公共变量)。
图9:插入的第一个数据 - 2.点击数据——合并文件——添加变量
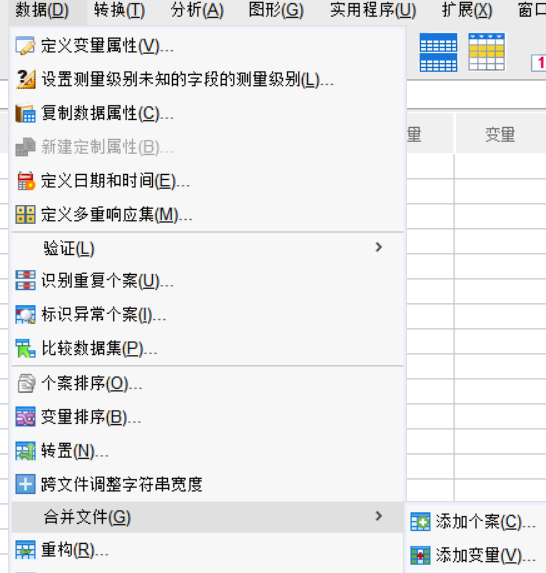
图10:合并步骤1 - 3.打开另一个数据集
有两种打开另一个数据文件的方式。
一种为打开数据集,需要事先在SPSS中打开另一个数据文件,此时就会在打开数据集的对话框中出现另一个数据文件,点击数据文件,继续即可。
另一种为点击外部SPSS Statistics数据文件,此方法无需事先打开另一数据文件,只需知道数据文件存放在哪里,在浏览里选择即可,最后点击继续。本次使用的是第二种。
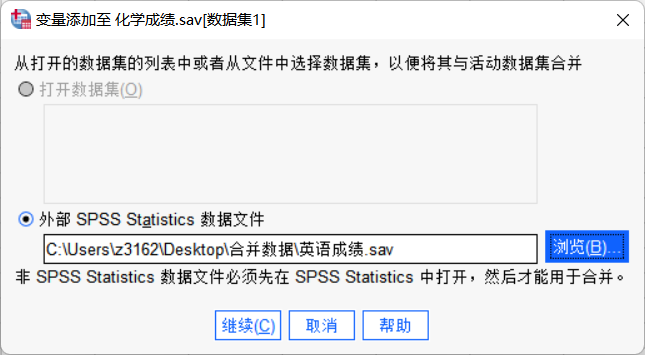
图10:插入第二个数据集 - 4.键变量设置
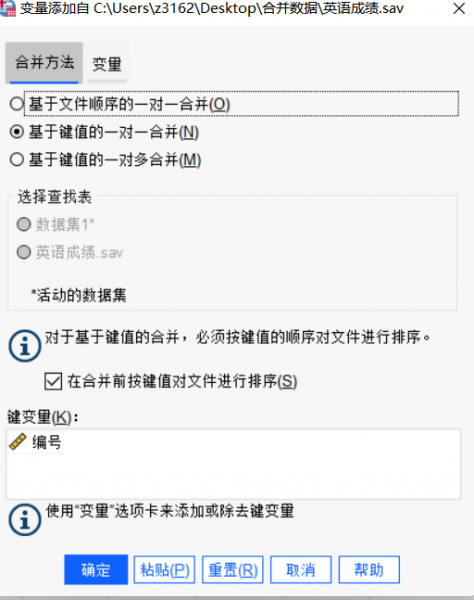
图11:设置1 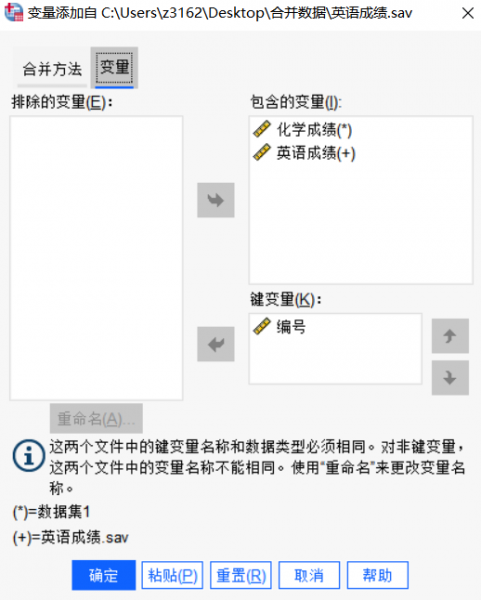
图12:设置2 - 5.根据自身数据情况设置完就可以合并。
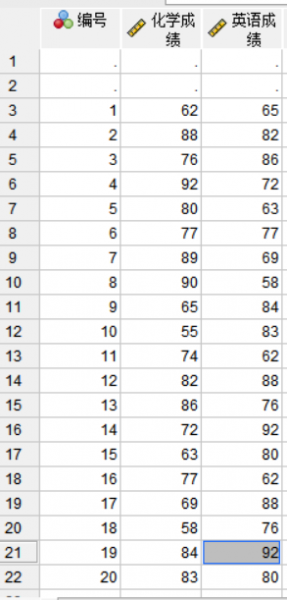
图13:合并成功图 三、SPSS的方差分析模型的优点
SPSS能够进行大多数统计分析(回归分析,logistic回归,生存分析,方差分析,因子分析,多变量分析)。SPSS能完成多种特殊效应的检验,进行多元方差分析,因子分析,判别分析等。操作简单,有一个类似于Excel的界面友好的数据编辑器,一定是分析数据路上的好帮手。
四、总结
以上就是这次带来的SPSS方差分析模型的参数估计 ,SPSS方差分析模型中两个变量合并。希望对大家有所帮助。
展开阅读全文
︾
标签:SPSS,IBM SPSS Statistics,单因素方差分析,多因素方差分析,方差分析,SPSS教程
读者也访问过这里:热门文章SPSS数据分析显著性差异分析步骤 SPSS显著性差异分析结果怎么看数据的显著性差异分析主要有三种方法,分别是卡方检验、T检验和方差分析。这三种方法都有具体的数据要求:卡方检验是对多个类别的数据进行分析,T检验是对两组数据进行分析,方差分析是对多组数据进行检验。下面,小编具体说明一下SPSS数据分析显著性差异分析步骤,SPSS显著性差异分析结果怎么看。2022-01-07实践SPSS单因素方差分析之检验结果解读在《实践SPSS单因素方差分析之变量与检验方法设置》一文中,我们已经详细地演示了IBM SPSS Statistics单因素方差分析方法的变量选择以及相关的选项、对比设置。2021-01-11spss如何做显著性分析 spss显著性差异分析怎么标abc在统计分析中,显著性分析是分析相关因素之间是否存在显著影响关系的关键性指标,通过它可以说明分析结论是否由抽样误差引起还是实际相关的,可论证分析结果的准确性。下面大家一起来看看用spss如何做显著性分析,spss显著性差异分析怎么标abc。2022-03-14SPSS回归分析中的f值是什么 SPSS回归分析F值在什么范围合适回归分析中以R表示相关性程度的高低,以F评价回归分析是否有统计学的意义,使用IBM SPSS Statistics进行回归分析,可以非常快速的完成R,F的计算,并且给出回归曲线方程,那么,SPSS回归分析中f值是什么?SPSS回归分析F值在什么范围合适,本文结合实例向大家作简单的说明。2022-07-22SPSS多元logistic回归分析的使用技巧回归分析是数据处理中较为常用的一类方法,它可以找出数据变量之间的未知关系,得到较为符合变量关系的数学表达式,以帮助用户完成数据分析。2021-04-26SPSS相关性分析结果怎么看相关性分析是对变量或个案之间相关度的测量,在SPSS中可以选择三种方法来进行相关性分析:双变量、偏相关和距离。2021-04-23最新文章SPSS多个自变量拟合怎么做 SPSS多个自变量相关性检验怎么做用过IBM SPSS Statistics软件的用户应该都清楚它的强大,我们可以用它来进行复杂数据分析,比如多个自变量拟合、相关性检验分析等等,而且软件界面相当友好,刚接触的小白也能快速掌握,本期我们就来介绍一下SPSS多个自变量拟合怎么做,SPSS多个自变量相关性检验怎么做的相关内容。2026-01-30SPSS做ks和sw正态性检验步骤 SPSS正态性检验ks和sw怎么看说到IBM SPSS Statistics,大家第一时间想到的可能就是它的专业统计功能。SPSS软件的数据处理与分析功能确实非常不错,很多科研、教育、市场研究等领域的用户都在使用。不过很多新手可能会觉得操作步骤复杂,其实不然。接下来我们就来带大家了解一下SPSS做ks和sw正态性检验步骤,SPSS正态性检验ks和sw怎么看的相关内容。2026-01-30SPSS非参数检验怎么测中位数 SPSS非参数检验z值的意义IBM SPSS Statistics这款软件对用户非常友好,例如非参数检验、数据随机性验证等统计分析,不需要复杂的操作,跟着步骤提示进行操作,即可快速生成统计结果表,新手也能快速掌握。今天我们就围绕SPSS非参数检验怎么测中位数,SPSS非参数检验z值的意义相关内容为大家展开介绍。2026-01-30SPSS随机值检验步骤 SPSS随机检验结果怎么看很多人都听过IBM SPSS Statistics这款软件,它是数据分析的可靠搭档,不仅能轻松搞定数据的整理、转换,最后还能自动生成图表,对新手非常友好。对于经常需要进行学术研究、市场调研的用户来说是个常用的选择。今天我们就来说一下SPSS随机值检验步骤,SPSS随机检验结果怎么看的相关内容。2026-01-30SPSS为什么没有事后检验 SPSS事后检验结果怎么看SPSS作为一款优秀的数据统计分析软件,深受数据统计分析人员的喜爱。SPSS之所以这么受欢迎,除了SPSS有很多的数据统计分析方法,可以帮助统计分析人员更高效的进行数据分析,还因为SPSS的人性化操作,一些刚入行的统计小白,也可以快速的掌握SPSS,接下来给大家详细介绍有关SPSS为什么没有事后检验,SPSS事后检验结果怎么看的相关内容。2026-01-30SPSS重复测量怎样分析 SPSS重复测量球形性应如何检验重复测量是数据分析中的一个重要环节。主要用来分析和检验数据样本中同一对象的相同指标在不同条件或者环境之下的变化情况,所以需要对这部分数据进行重复的测量和分析。例如我们统计一组大学生毕业后的就业情况,那么大学生的专业分类和性别都一致的情况下,就需要分析不同的就业影响因素对于最后就业率的影响。下面给大家介绍SPSS重复测量应当怎样分析,SPSS重复测量球形性应如何检验。2026-01-14微信公众号
欢迎加入 SPSS 产品的大家庭,立即扫码关注,获取更多软件动态和资源福利。
读者也喜欢这些内容:
-
SPSS如何把多个指标合并成一个变量 如何定义SPSS变量属性
对于科研工作者、数据分析师来说,好用的数据分析软件可以帮助我们显著提高工作效率。SPSS既能够帮助我们进行日常的数据分析,还可以依照数据分析的结果给出相应的数据分析报告,辅助我们进行后续的工作。接下来给大家介绍SPSS如何把多个指标合并成一个变量,如何定义SPSS变量属性的具体内容。...
阅读全文 >
-
SPSS计算平均值公式 SPSS怎么计算变异系数
SPSS是一款用于数据统计分析的软件,被广泛应用于学术和商业分析等多个领域。计算平均值、变异系数、方差和标准差等等是SPSS的基础功能,平均值是我们经常提到的一项数据,大家并不陌生,但是大家可能对变异系数并不熟悉,简单来说变异系数用于比较单位或平均数不同的两个或多个数据组差别程度,计算公式是标准差除以平均数。接下来我就详细地给大家介绍一下关于SPSS计算平均值公式,SPSS怎么计算变异系数的相关内容。...
阅读全文 >
-
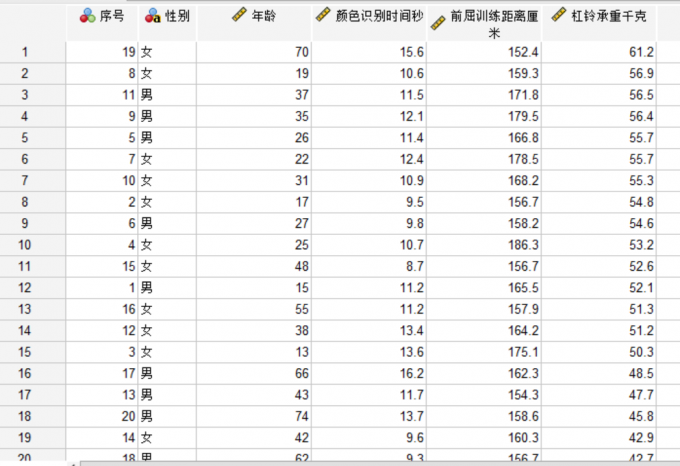
SPSS数据转置什么意思 SPSS数据转置怎么操作
在进行SPSS数据计算和分析之前,研究者通常运用SPSS数据转置的方法,借此对繁杂数据进行行列互换,适用于EXCEL、CSV、文本数据、SAS等各类形式的数据文本,便于研究者清晰全面地了解数据信息。本文以SPSS数据转置什么意思,SPSS数据转置怎么操作这两个问题为例,带大家了解一下SPSS数据转置的相关知识。...
阅读全文 >
-
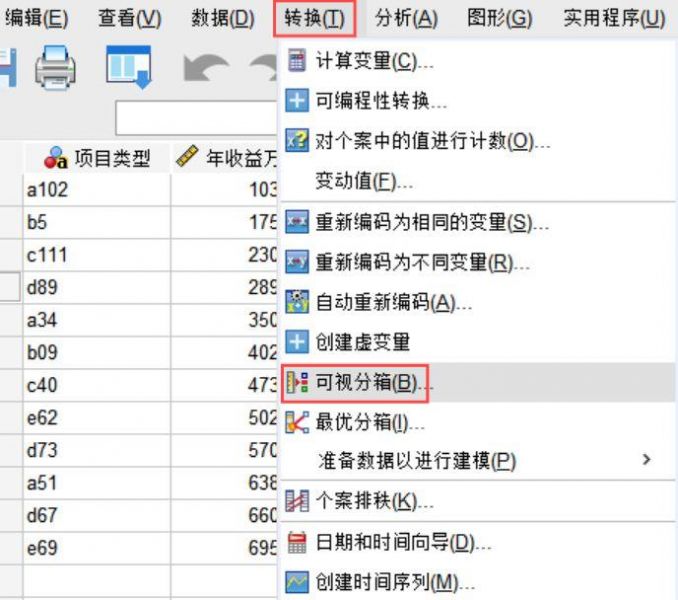
SPSS可视化分箱是什么意思 SPSS可视化分箱点了不显示
当需要对繁杂数据组进行分类且可视化的图表呈现,我们可以使用SPSS可视化分箱的功能应用来实现上述需求,这样既能获取清晰直观的数据示例图,还可以便利后续的研究数据分析。今天,我们以SPSS可视化分箱是什么意思,SPSS可视化分箱点了不显示这两个问题为例,带大家了解SPSS可视化分箱的相关知识。...
阅读全文 >





