


- 首页
- 产品
- 下载
-
帮助中心
SPSS怎么分析数据规律 SPSS数据分析如何有效使用
发布时间:2024-12-26 17: 06: 00
电脑型号:联想ThinkBook 16+
软件版本:windows10 64位旗舰版
系统:IBM SPSS Statistics 27
在撰写论文或者报告时,会涉及到收集、分析数据,当拿到数据后,怎么查看数据规律以及怎么分析数据对论文结果很重要。本文会告诉大家SPSS怎么分析数据规律,SPSS数据分析如何有效使用。
一、SPSS怎么分析数据规律
1. 描述性统计分析
描述性统计分析中的频率和描述分析不仅可以用来计算数据的平均值、中位数、标准差等指标,还可以制作直方图、散点图、箱线图等图表来直观地呈现数据的分布情况。通过频率和描述分析可以看到数据的集中趋势、离散程度以及分布特征(如偏度和峰度)。直方图可以展示数值的频数分布情况;饼图可以展示不同数值的占比情况;条形图则可以对比不同数值之间的差异。
描述性统计分析中的探索分析不光可以计算数据平均值、中位数、最大值和最小值等,还能进一步进行参数估计和假设检验。
描述性统计分析中的交叉表,即(交叉频数分布)可以分析两个或多个变量之间的关系,以及它们的联合分布情况。
2.相关分析和回归分析
相关分析用来探讨变量之间的关系,计算相关系数来描述它们之间的关系强度和方向。
回归分析用来探讨自变量和因变量之间的关系,建立模型并预测因变量的值,从而探讨自变量对因变量的影响程度。
3.因子分析和主成分分析
因子分析和主成分分析都是统计学中常用的降维技术,它们可以帮助我们从高维数据中提取出最重要的特征,以简化模型并提高分析效率。
二、SPSS数据分析如何有效使用
上面我们讲了SPSS怎么分析数据规律,那么接下来就涉及到怎么在SPSS中有效的分析数据,即SPSS数据分析如何有效使用。
分析所使用的数据包含性别(定性变量)、年级(定性变量)、实习次数(定量变量)以及期望工资(定量变量)。
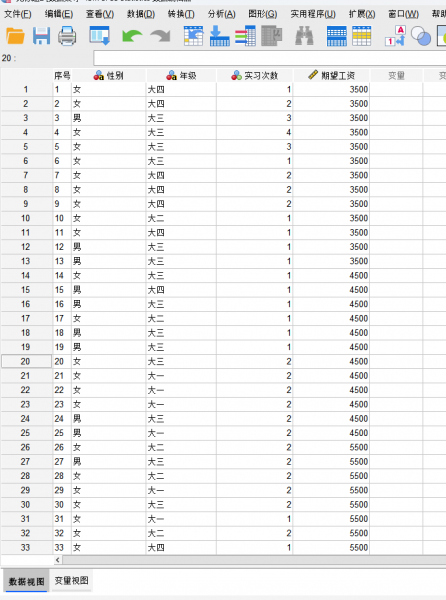
图1 数据来源 1.描述性统计分析
①我们首先按照下图顺序进行频率分析,这是针对定量变量的分析操作。
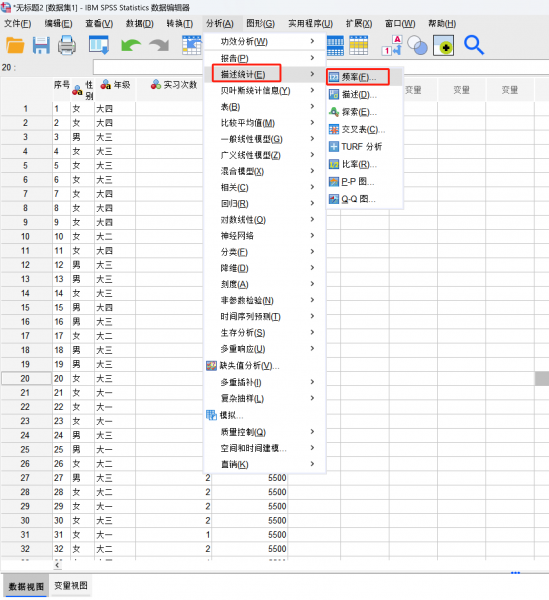
图2 频率分析 ②将“实习次数”以及“期望工资”这两个定量变量纳入,再将相应的描述指标勾选上,这里可以多勾选几个,方便我们后续观察数据规律。
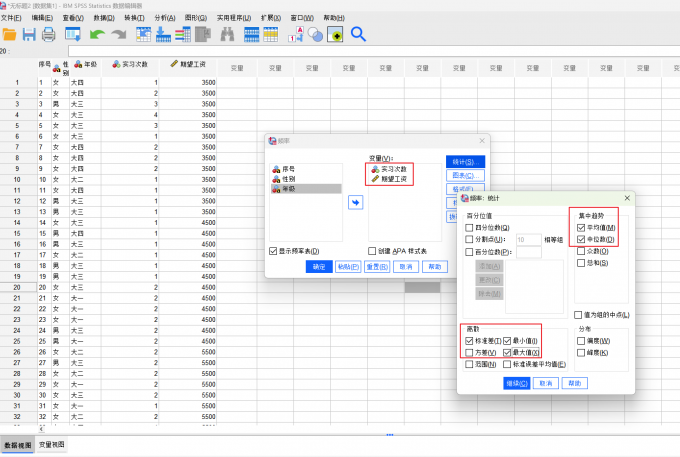
图3 频率分析 ③在“图表”中勾选“饼图”。因为这里我们想看各部分的占比,当然用户在自己操作时可以挨着将条形图、饼图、直方图都勾选一次查看数据规律。
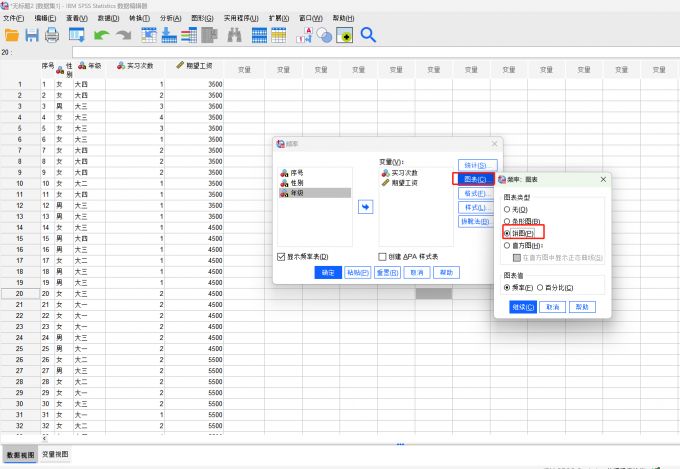
图4 图形选择 ④在输出结果中可以看到,“实习次数”和“期望工资”的平均值,最小值等。在频率表里面还可以看到各部分的百分比。
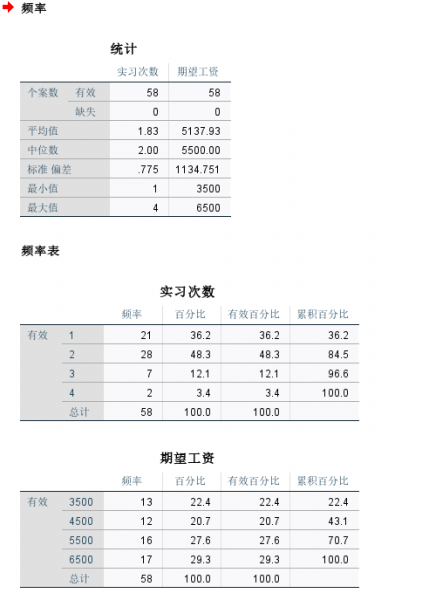
图5 输出结果 ⑤饼图结果中,上方的标题就是对应的变量,这里时“实习次数”,每个图中还可以显示百分比。饼图更能直观的看出数据的分布状况,这里实习次数为2的占比最大,为28%。
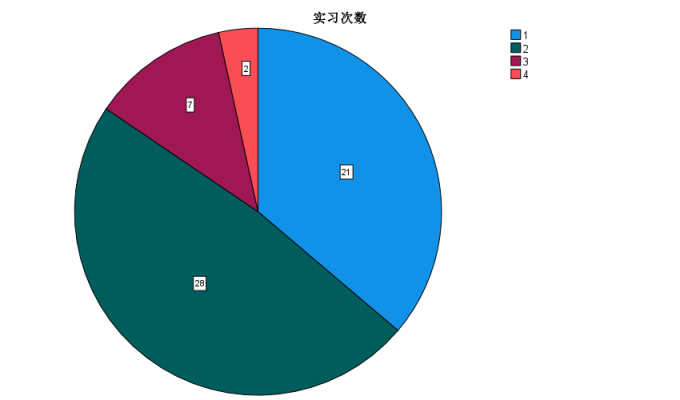
图6 饼图结果 2.相关分析和回归分析
由于SPSS里面只能使用数字进行分析,所以我们要先对文字部分进行重新编码,有关编码部分读者可以自行搜索相关内容,这里不再阐述。下图为将“性别”和“年级”重新编码的变量。
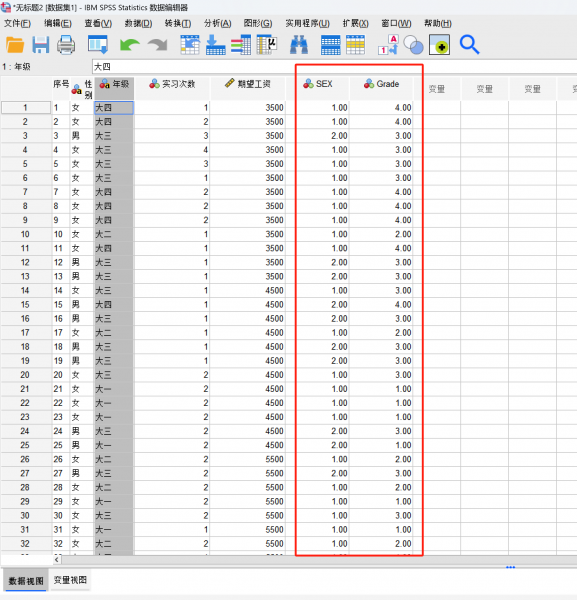
图7 重新编码视图 ①观察两两变量是否相关,可以点击“相关”中的“双变量”进行分析。
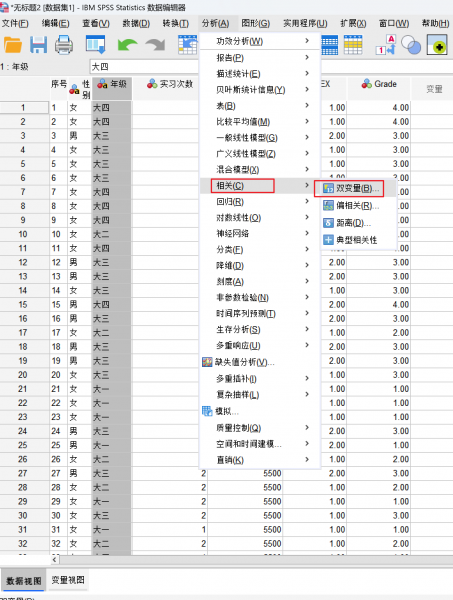
图8 相关分析 ②为了更广泛的探索变量间的相关关系,我们建议将所有变量(不多的情况下)统一纳入分析。
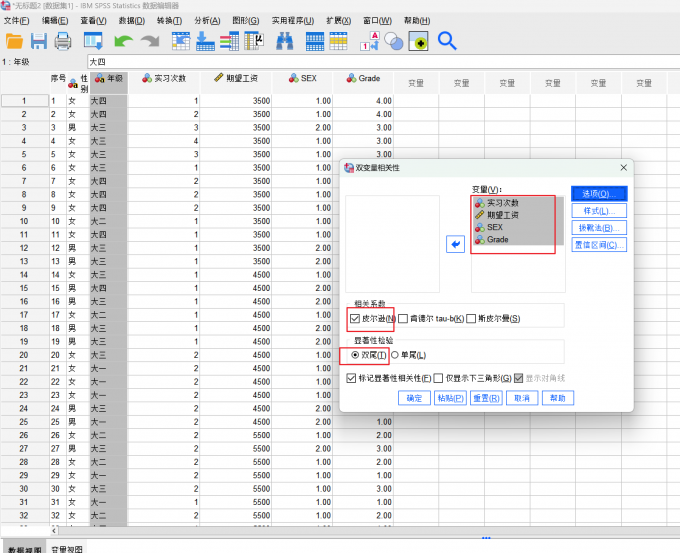
图9 双变量相关分析 ③通过输出结果中,带*号(表示两变量相关)的数据可以看出,期望工资和性别有关,且期望工资也和年级有关。
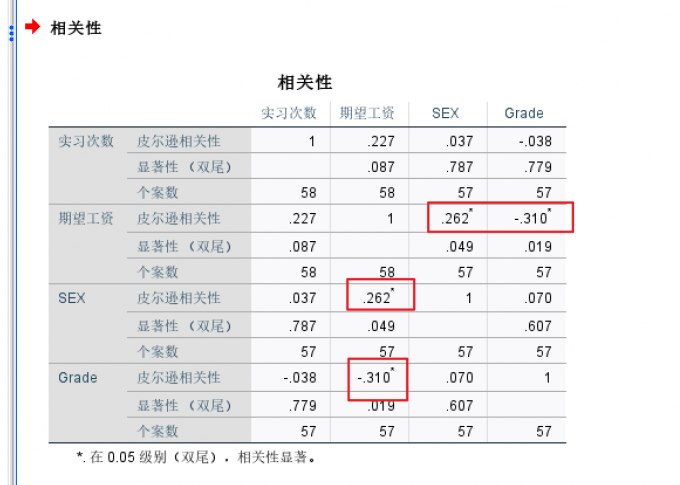
图10 相关分析结果 ④在进行了上面的相关分析确定哪些变量间有相关关系后,下一步可以进行回归分析。
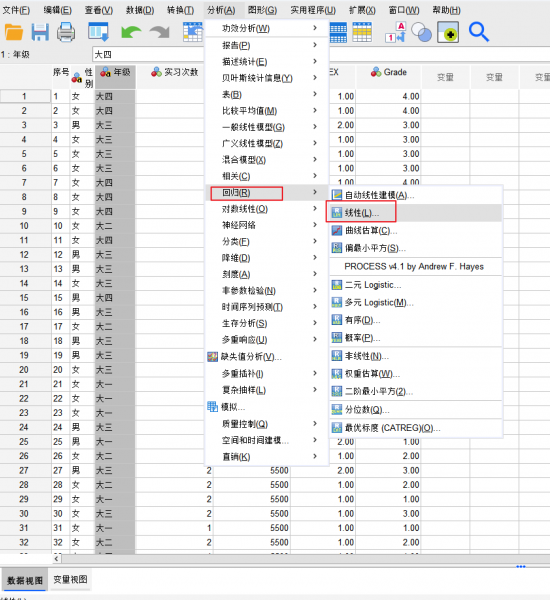
图11 线性回归操作 ⑤因为“期望工资”同时和两个变量相关,因此我们可以初步将“期望工资”定为因变量,”“性别”和“年级”作为自变量纳入线性回归方程。
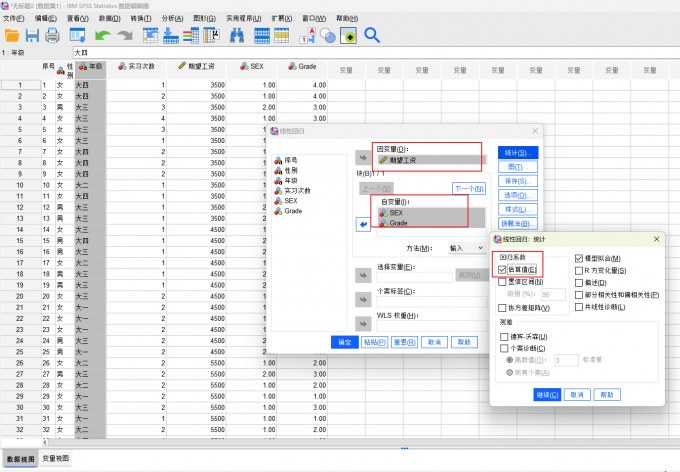
图12 线性回归操作 ⑥在回归方程的结果输出中,通过看“显著性”一列,发现编码后的“性别”和“年级”的显著性值均小于005,说明这两个变量都对期望工资具有影响。且通过看“B”这一列的正负号可以得出,男生比女生的期望工资更高,高年级比低年级的期望工资更低。
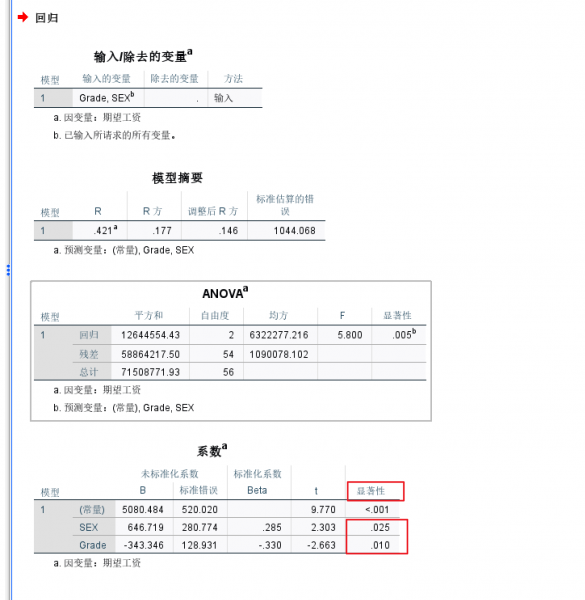
图13 线性回归结果 3.因子分析和主成分分析
因子分析通过“降维”→“因子”进行分析,见下图。其余的相关具体操作步骤读者可以自行搜索,因涉及篇幅过长,这里不过多阐述。
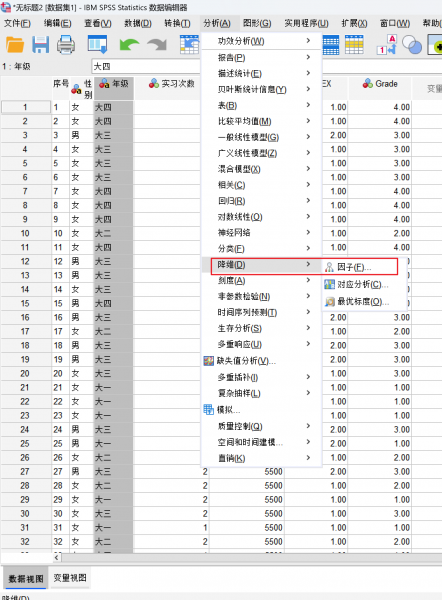
图14 因子分析操作 本文讲解了SPSS怎么分析数据规律中的三个主要分析方法,包括描述统计,相关和回归,因子分析和主成分分析,以及如何在SPSS中具体操作前两种方法,并且介绍了怎么解读输出结果。以上就是SPSS怎么分析数据规律 SPSS数据分析如何有效使用的全部内容,希望能帮助到有需要的小伙伴。
展开阅读全文
︾
标签:数据统计分析软件,数据分析软件
读者也访问过这里:热门文章SPSS数据分析显著性差异分析步骤 SPSS显著性差异分析结果怎么看数据的显著性差异分析主要有三种方法,分别是卡方检验、T检验和方差分析。这三种方法都有具体的数据要求:卡方检验是对多个类别的数据进行分析,T检验是对两组数据进行分析,方差分析是对多组数据进行检验。下面,小编具体说明一下SPSS数据分析显著性差异分析步骤,SPSS显著性差异分析结果怎么看。2022-01-07实践SPSS单因素方差分析之检验结果解读在《实践SPSS单因素方差分析之变量与检验方法设置》一文中,我们已经详细地演示了IBM SPSS Statistics单因素方差分析方法的变量选择以及相关的选项、对比设置。2021-01-11spss如何做显著性分析 spss显著性差异分析怎么标abc在统计分析中,显著性分析是分析相关因素之间是否存在显著影响关系的关键性指标,通过它可以说明分析结论是否由抽样误差引起还是实际相关的,可论证分析结果的准确性。下面大家一起来看看用spss如何做显著性分析,spss显著性差异分析怎么标abc。2022-03-14SPSS回归分析中的f值是什么 SPSS回归分析F值在什么范围合适回归分析中以R表示相关性程度的高低,以F评价回归分析是否有统计学的意义,使用IBM SPSS Statistics进行回归分析,可以非常快速的完成R,F的计算,并且给出回归曲线方程,那么,SPSS回归分析中f值是什么?SPSS回归分析F值在什么范围合适,本文结合实例向大家作简单的说明。2022-07-22SPSS多元logistic回归分析的使用技巧回归分析是数据处理中较为常用的一类方法,它可以找出数据变量之间的未知关系,得到较为符合变量关系的数学表达式,以帮助用户完成数据分析。2021-04-26SPSS相关性分析结果怎么看相关性分析是对变量或个案之间相关度的测量,在SPSS中可以选择三种方法来进行相关性分析:双变量、偏相关和距离。2021-04-23最新文章SPSS非参数检验怎么测中位数 SPSS非参数检验z值的意义IBM SPSS Statistics这款软件对用户非常友好,例如非参数检验、数据随机性验证等统计分析,不需要复杂的操作,跟着步骤提示进行操作,即可快速生成统计结果表,新手也能快速掌握。今天我们就围绕SPSS非参数检验怎么测中位数,SPSS非参数检验z值的意义相关内容为大家展开介绍。2026-01-30SPSS随机值检验步骤 SPSS随机检验结果怎么看很多人都听过IBM SPSS Statistics这款软件,它是数据分析的可靠搭档,不仅能轻松搞定数据的整理、转换,最后还能自动生成图表,对新手非常友好。对于经常需要进行学术研究、市场调研的用户来说是个常用的选择。今天我们就来说一下SPSS随机值检验步骤,SPSS随机检验结果怎么看的相关内容。2026-01-30SPSS为什么没有事后检验 SPSS事后检验结果怎么看SPSS作为一款优秀的数据统计分析软件,深受数据统计分析人员的喜爱。SPSS之所以这么受欢迎,除了SPSS有很多的数据统计分析方法,可以帮助统计分析人员更高效的进行数据分析,还因为SPSS的人性化操作,一些刚入行的统计小白,也可以快速的掌握SPSS,接下来给大家详细介绍有关SPSS为什么没有事后检验,SPSS事后检验结果怎么看的相关内容。2026-01-30SPSS重复测量怎样分析 SPSS重复测量球形性应如何检验重复测量是数据分析中的一个重要环节。主要用来分析和检验数据样本中同一对象的相同指标在不同条件或者环境之下的变化情况,所以需要对这部分数据进行重复的测量和分析。例如我们统计一组大学生毕业后的就业情况,那么大学生的专业分类和性别都一致的情况下,就需要分析不同的就业影响因素对于最后就业率的影响。下面给大家介绍SPSS重复测量应当怎样分析,SPSS重复测量球形性应如何检验。2026-01-14SPSS亚组分析的注意事项 SPSS亚组分析结果解读对于经常与数据分析打交道的小伙伴来说,想必对亚组分析这个概念应该不会感到陌生。亚组分析是用来检测异质性结果的方法之一,亚组分析的数据结果分为确证性、支持性和探索性三类。而我们在进行亚组分析时,可以借助数据分析软件SPSS的帮助,它一方面可以帮助我们得到亚组分析的数据结果,还能够把这些数据分析结果以报告形成呈现出来。接下来给大家介绍SPSS亚组分析的注意事项, SPSS亚组分析结果解读的具体内容。2026-01-14SPSS卡方检验样本不满足要求怎么办 卡方检验SPSS结果都小于0.5说明了什么在数据分析的过程中,卡方样本检验是常见的一种统计方式。卡方检验主要用来检验数据样本之间的离散程度,进而判断不同数据之间的偏差值,如果数据样本在统计的时候不符合实际的统计需求,就可能导致卡方检验不满足要求。所以我们需要在统计的过程中对数据样本和统计方法进行调整,这样能够规避数据样本检验带来的结果偏差风险。下面以SPSS为例,给大家介绍SPSS卡方检验样本不满足要求怎么办,卡方检验SPSS结果都小于0.5说明了什么的具体内容。2026-01-14微信公众号
欢迎加入 SPSS 产品的大家庭,立即扫码关注,获取更多软件动态和资源福利。
读者也喜欢这些内容:
-
SPSS趋势卡方怎么做 SPSS趋势卡方检验怎么看正相关
趋势卡方是SPSS中检验变量相关性的方法之一,当我们的分析数据中存在多个变量时,就可以使用趋势卡方来检验这些变量是否相互关联、相互影响。检验完毕后,我们也可以根据这些检验结果来选择更加合适的数据分析模型。今天我就以SPSS趋势卡方怎么做,SPSS趋势卡方检验怎么看正相关这两个问题为例,来向大家讲解一下趋势卡方的相关知识。...
阅读全文 >
-
SPSS显著性小于0.001的意义 SPSS显著性大于0.05怎么办
在使用SPSS软件进行数据分析工作的过程中,得到的显著性水平分析结果具有极为重要的作用。它能够帮助我们衡量变量之间是否存在真实的关联,或者不同组别数据之间是否存在实质性的差异。今天我们就一起来探讨关于SPSS显著性小于0.001的意义,SPSS显著性大于0.05怎么办的问题。...
阅读全文 >
-
SPSS多重响应交叉表怎么做 SPSS多重响应交叉表结果解读
多重响应交叉表工具是数据分析工作中较为常见的一种分析模型,我们可以使用交叉表工具来探究两个变量之间的关联性。今天我就以SPSS多重响应交叉表怎么做,SPSS多重响应交叉表结果解读这两个问题为例,来向大家讲解一下多重响应交叉表的相关知识。...
阅读全文 >
-
SPSS怎么计算偏度系数和峰度系数 SPSS中偏度和峰度的判断标准分别是什么
偏度和峰度是判断数据是否符合正态分布的重要标准之一,我们在进行数据分析之前,都会通过这两个参数来检验数据文档的合理性。今天我就以SPSS怎么计算偏度系数和峰度系数,SPSS中偏度和峰度的判断标准分别是什么这两个问题为例,来向大家讲解一下偏度和峰度的相关知识。...
阅读全文 >
-



















