


- 首页
- 产品
- 下载
-
帮助中心
SPSS如何把多个题项变成一个维度 SPSS如何把多个题项分析出来
发布时间:2025-06-27 10: 40: 00
品牌型号:联想ThinkBook
系统:windows10 64位旗舰版
软件版本:IBM SPSS Statistics 29.0
在回收调查问卷的数据后,研究者通常会对问卷中相关性较高的题项进行合并,这就需要运用到SPSS转换和计算变量的函数指令方法,从而使多个问卷题项变成一个维度来计算均值结果。本文以SPSS如何把多个题项变成一个维度,SPSS如何把多个题项分析出来这两个问题为例,带大家了解一下SPSS多题项合并的知识。
一、SPSS如何把多个题项变成一个维度
在把复杂题项变化为一个维度之前,我们需要先判断这些题项之间是否存在相关性,也就是多个题目是否在同一主题范围,例如心理状态、身体情况、工作因素、经济收入等等。如果多个题项都能够被划定在同类主题范围,我们就可以将这些题项通过SPSS函数指令来合并为一个新的变量。
1、下图是2024年对某地居民生活情况的问卷调查,涉及受访者性别、年龄、学历、年收入、媒体使用情况等多方面的数据信息,这里以媒体使用情况为例,调查者想要了解该地居民在2024年整体的媒体使用频率,所以需要对报纸、杂志、广播、电视、互联网、电影等媒介题项进行同一维度的合并。
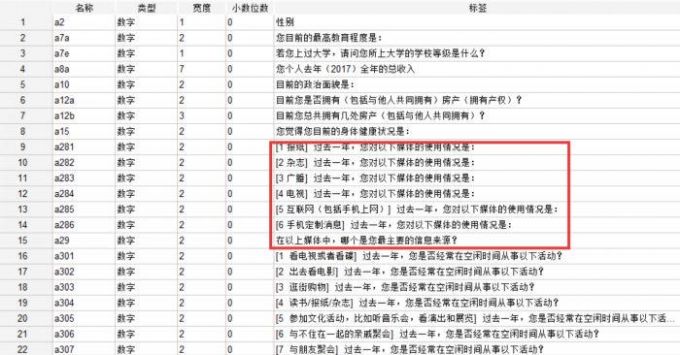
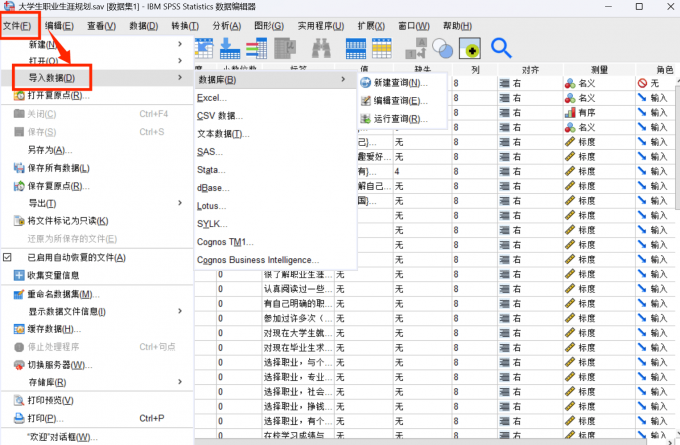
图1:2024年某地居民生活普查数据 2、接下来找到SPSS应用功能栏的转换按键,选择【计算变量】的选项模块,由此便能够将想要合并的题项汇总在一起,并且以均值方式进行变量计算,然后再命名新的目标变量。
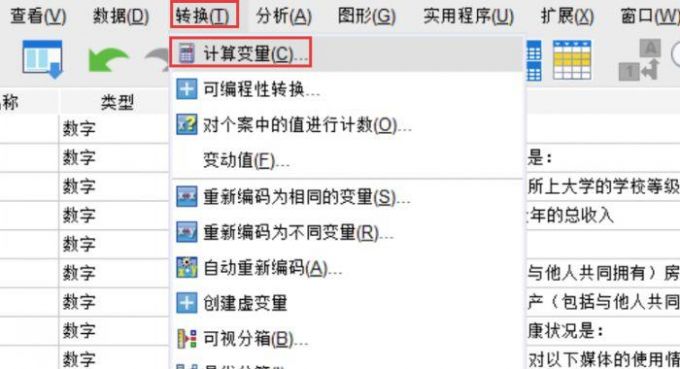
图2:转换模块的计算变量 3、在下图右侧的函数组内容栏,我们找到计算数据均值的Mean函数指令,然后把该函数指令放入上方的数字表达式之中,现今显示的问号代表待放入的问卷题项。根据案例题项的主题,我们在与数字表达式对应的目标变量名称填入媒体使用频率。
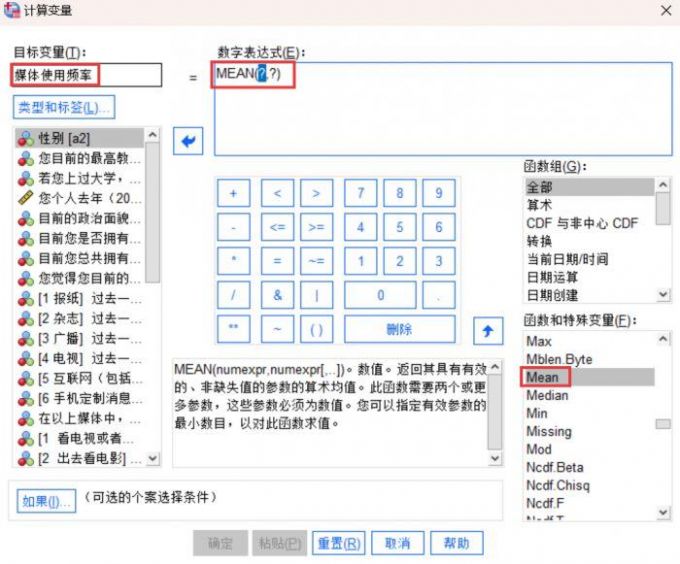
图3:均值函数的数字表达式 4、因为想要了解该地居民2024年整体的媒体使用频率,所以把代表报纸、杂志、广播、电视、互联网、电影的a281、a282、a283、a284、a285、a302这六个题项放入数字表达式的Mean函数括号内,注意这些题项以英文逗号的标点符号格式来间隔。
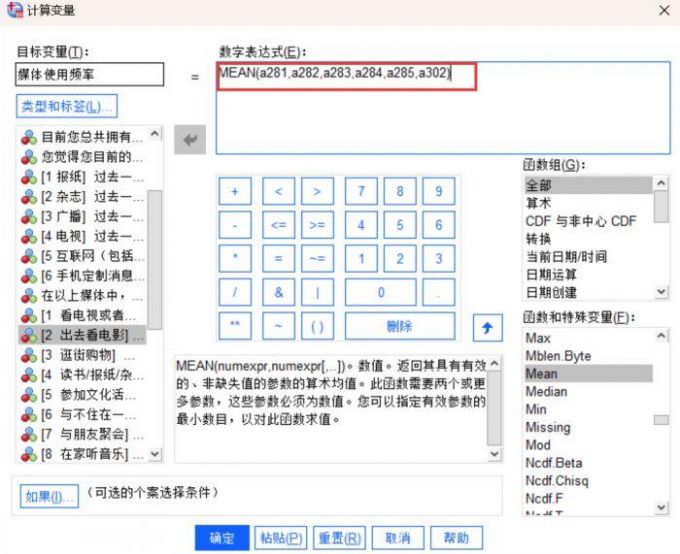
图4:Mean函数代入六个题项 5、按照上述操作流程,我们可以在变量的数据视图看到最后一列的新变量,也就是a281、a282、a283、a284、a285、a302这六个题项合并的媒体使用频率的新维度,能够看到下图的媒体使用频率有3.33、3.67、2.83、2.67等等多个数值,代表报纸、杂志、广播、电视、互联网、电影的综合使用均值。
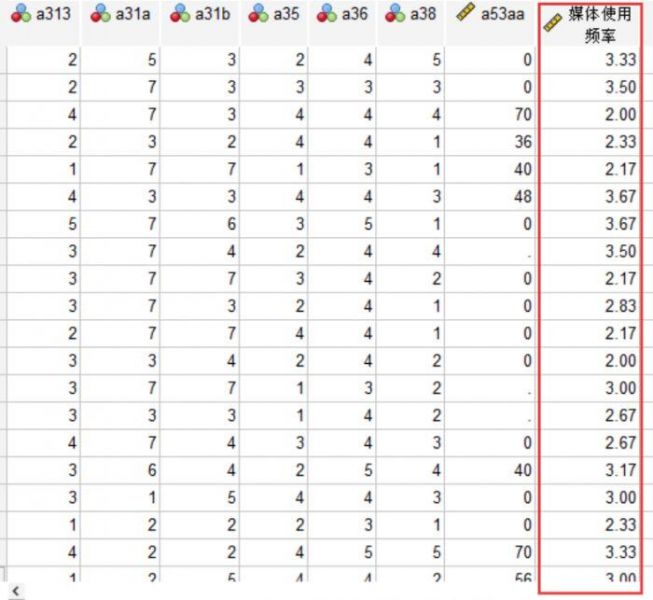
图5:媒体使用频率的数值结果 二、SPSS如何把多个题项分析出来
当通过SPSS计算变量的功能按键把多个题项变为一个维度,我们可以采用因素分析或者主成分分析的方法,然后对得到的综合维度进行相关分析,这需要了解和掌握问卷题项的综合主题是什么以及是否适合放在同一内容维度。
1、我们再以某事业单位公务人员的工作情况调查为例,该单位想要了解被调查者整体的工作情况,所以需要把报酬收入、福利待遇、工作中的自主程度、工作的社会影响、工作的成就感、工作中主动创新的机会这些题项合并为一个维度。
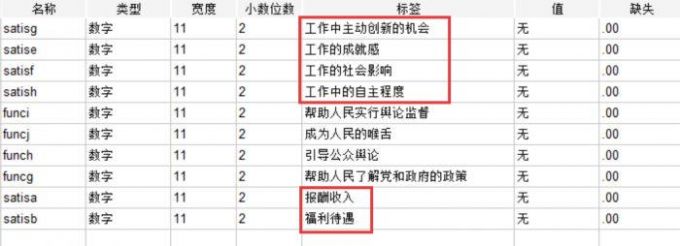
图6:某单位公务人员的工作情况调查 2、接下来把报酬收入、福利待遇、工作中的自主程度、工作的社会影响、工作的成就感、工作中主动创新的机会这六个题项放入数字表达式的Mean函数括号内,注意这些题项以英文逗号的标点符号格式来间隔。
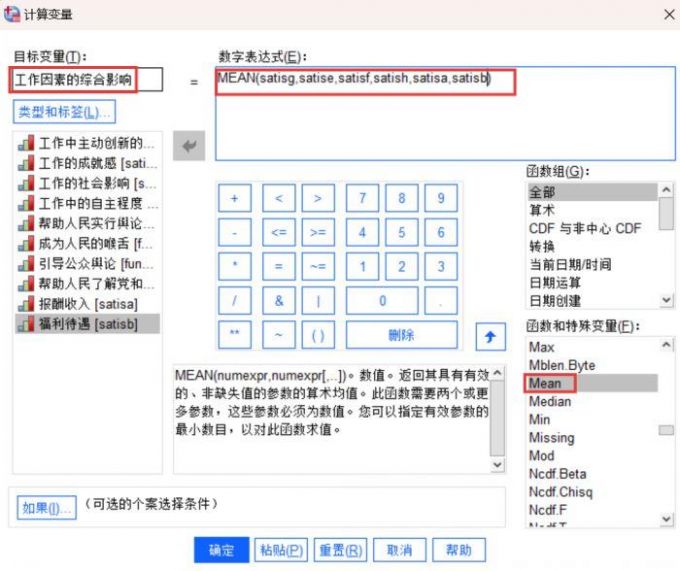
图7:工作因素的综合影响作为目标变量 3、根据Mean函数的指令设置,我们可以在变量的数据视图看到最后一列的新变量,也就是上述六个题项合并的“工作因素的综合影响”,能够看到新变量数据有2.83、3.17、1.67、1.33、2.67等等多个数值,代表报酬收入、福利待遇、工作中的自主程度、工作的社会影响、工作的成就感、工作中主动创新的机会的综合影响。
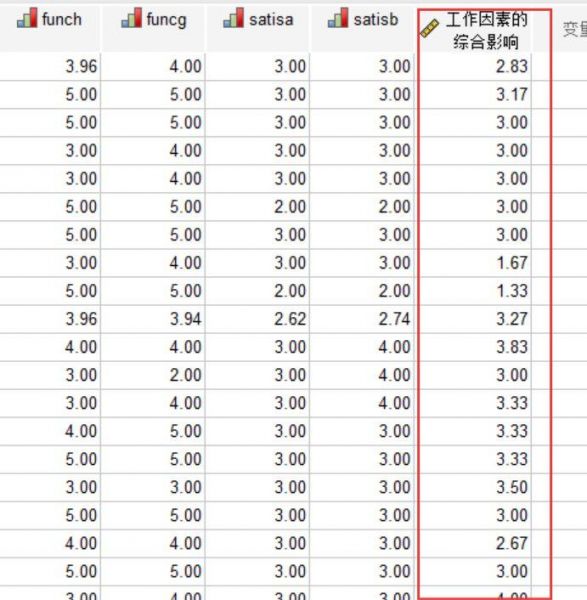
图8:多题项的综合影响数值 三、小结
以上就是SPSS如何把多个题项变成一个维度,SPSS如何把多个题项分析出来的解答。如果想要对多个题项进行综合意义分析,推荐使用SPSS转换和计算变量的功能进行操作。最后,也欢迎大家前往SPSS的中文网站,学习更多关于数据分析的操作技巧。
展开阅读全文
︾
标签:SPSS下载,SPSS下载教程
读者也访问过这里:热门文章SPSS数据分析显著性差异分析步骤 SPSS显著性差异分析结果怎么看数据的显著性差异分析主要有三种方法,分别是卡方检验、T检验和方差分析。这三种方法都有具体的数据要求:卡方检验是对多个类别的数据进行分析,T检验是对两组数据进行分析,方差分析是对多组数据进行检验。下面,小编具体说明一下SPSS数据分析显著性差异分析步骤,SPSS显著性差异分析结果怎么看。2022-01-07实践SPSS单因素方差分析之检验结果解读在《实践SPSS单因素方差分析之变量与检验方法设置》一文中,我们已经详细地演示了IBM SPSS Statistics单因素方差分析方法的变量选择以及相关的选项、对比设置。2021-01-11spss如何做显著性分析 spss显著性差异分析怎么标abc在统计分析中,显著性分析是分析相关因素之间是否存在显著影响关系的关键性指标,通过它可以说明分析结论是否由抽样误差引起还是实际相关的,可论证分析结果的准确性。下面大家一起来看看用spss如何做显著性分析,spss显著性差异分析怎么标abc。2022-03-14SPSS回归分析中的f值是什么 SPSS回归分析F值在什么范围合适回归分析中以R表示相关性程度的高低,以F评价回归分析是否有统计学的意义,使用IBM SPSS Statistics进行回归分析,可以非常快速的完成R,F的计算,并且给出回归曲线方程,那么,SPSS回归分析中f值是什么?SPSS回归分析F值在什么范围合适,本文结合实例向大家作简单的说明。2022-07-22SPSS多元logistic回归分析的使用技巧回归分析是数据处理中较为常用的一类方法,它可以找出数据变量之间的未知关系,得到较为符合变量关系的数学表达式,以帮助用户完成数据分析。2021-04-26SPSS相关性分析结果怎么看相关性分析是对变量或个案之间相关度的测量,在SPSS中可以选择三种方法来进行相关性分析:双变量、偏相关和距离。2021-04-23最新文章SPSS非参数检验怎么测中位数 SPSS非参数检验z值的意义IBM SPSS Statistics这款软件对用户非常友好,例如非参数检验、数据随机性验证等统计分析,不需要复杂的操作,跟着步骤提示进行操作,即可快速生成统计结果表,新手也能快速掌握。今天我们就围绕SPSS非参数检验怎么测中位数,SPSS非参数检验z值的意义相关内容为大家展开介绍。2026-01-30SPSS随机值检验步骤 SPSS随机检验结果怎么看很多人都听过IBM SPSS Statistics这款软件,它是数据分析的可靠搭档,不仅能轻松搞定数据的整理、转换,最后还能自动生成图表,对新手非常友好。对于经常需要进行学术研究、市场调研的用户来说是个常用的选择。今天我们就来说一下SPSS随机值检验步骤,SPSS随机检验结果怎么看的相关内容。2026-01-30SPSS为什么没有事后检验 SPSS事后检验结果怎么看SPSS作为一款优秀的数据统计分析软件,深受数据统计分析人员的喜爱。SPSS之所以这么受欢迎,除了SPSS有很多的数据统计分析方法,可以帮助统计分析人员更高效的进行数据分析,还因为SPSS的人性化操作,一些刚入行的统计小白,也可以快速的掌握SPSS,接下来给大家详细介绍有关SPSS为什么没有事后检验,SPSS事后检验结果怎么看的相关内容。2026-01-30SPSS重复测量怎样分析 SPSS重复测量球形性应如何检验重复测量是数据分析中的一个重要环节。主要用来分析和检验数据样本中同一对象的相同指标在不同条件或者环境之下的变化情况,所以需要对这部分数据进行重复的测量和分析。例如我们统计一组大学生毕业后的就业情况,那么大学生的专业分类和性别都一致的情况下,就需要分析不同的就业影响因素对于最后就业率的影响。下面给大家介绍SPSS重复测量应当怎样分析,SPSS重复测量球形性应如何检验。2026-01-14SPSS亚组分析的注意事项 SPSS亚组分析结果解读对于经常与数据分析打交道的小伙伴来说,想必对亚组分析这个概念应该不会感到陌生。亚组分析是用来检测异质性结果的方法之一,亚组分析的数据结果分为确证性、支持性和探索性三类。而我们在进行亚组分析时,可以借助数据分析软件SPSS的帮助,它一方面可以帮助我们得到亚组分析的数据结果,还能够把这些数据分析结果以报告形成呈现出来。接下来给大家介绍SPSS亚组分析的注意事项, SPSS亚组分析结果解读的具体内容。2026-01-14SPSS卡方检验样本不满足要求怎么办 卡方检验SPSS结果都小于0.5说明了什么在数据分析的过程中,卡方样本检验是常见的一种统计方式。卡方检验主要用来检验数据样本之间的离散程度,进而判断不同数据之间的偏差值,如果数据样本在统计的时候不符合实际的统计需求,就可能导致卡方检验不满足要求。所以我们需要在统计的过程中对数据样本和统计方法进行调整,这样能够规避数据样本检验带来的结果偏差风险。下面以SPSS为例,给大家介绍SPSS卡方检验样本不满足要求怎么办,卡方检验SPSS结果都小于0.5说明了什么的具体内容。2026-01-14微信公众号
欢迎加入 SPSS 产品的大家庭,立即扫码关注,获取更多软件动态和资源福利。
读者也喜欢这些内容:
-
SPSS怎么进行描述性统计分析 SPSS均值标准差计算步骤
在统计学当中,描述性分析主要用来对调查样本总体的数据进行相关描述性质的研究(比如用图形的方式描述分析)。而在进行描述性分析的时候,我经常会用到SPSS数据分析软件,这款软件给我提供了许多数据分析的帮助。接下来给大家介绍SPSS怎么进行描述性统计分析,SPSS均值标准差计算步骤的具体内容。...
阅读全文 >
-
SPSS ROC阈值怎样确定 SPSS ROC阈值选择导致敏感度过低怎么办
说到阈值分析,我们脑海中可能会想到常规的寻找阈值关键临界点的分析方式(例如在医学当中会通过阈值分析的方式来确定药物在病人体内生效的时间临界点)。但是在有些分析场景中,就需要用到ROC曲线作为阈值分析的工具,ROC曲线作为阈值分析中的一个重要工具,可以用来找到数据点位发生明显截断变化的临界点。下面以SPSS为例,给大家介绍SPSS ROC阈值怎样确定,SPSS ROC阈值选择导致敏感度过低怎么办。...
阅读全文 >
-
SPSS趋势卡方怎么做 SPSS趋势卡方检验怎么看正相关
趋势卡方是SPSS中检验变量相关性的方法之一,当我们的分析数据中存在多个变量时,就可以使用趋势卡方来检验这些变量是否相互关联、相互影响。检验完毕后,我们也可以根据这些检验结果来选择更加合适的数据分析模型。今天我就以SPSS趋势卡方怎么做,SPSS趋势卡方检验怎么看正相关这两个问题为例,来向大家讲解一下趋势卡方的相关知识。...
阅读全文 >
-
SPSS怎么绘制柱状图 SPSS图表编辑器使用技巧
由于数据分析领域经常需要庞大的数据样本,所以将数据图像化便是其中的一项重要任务。因此绘制数据分析图便成为了其中的关键操作。SPSS作为一款专业的数据分析软件,不仅可以用它来处理日常的各种数据分析内容,还能够完成数据图像的绘制和图表的编译。接下来给大家介绍SPSS怎么绘制柱状图,SPSS图表编辑器使用技巧的具体内容。...
阅读全文 >
-













