


- 首页
- 产品
- 下载
-
帮助中心
spss多元线性回归分析操作步骤,spss多元线性回归分析结果解读
发布时间:2022-05-07 16: 26: 50
品牌型号:联想GeekPro 2020
系统: Windows 10 64位专业版
软件版本: IBM SPSS Statistics
spss多元线性回归分析操作步骤,本文会以客流量、销售量与销售额的线性关系演示spss的多元线性回归分析操作步骤,并进行spss多元线性回归分析结果解读。
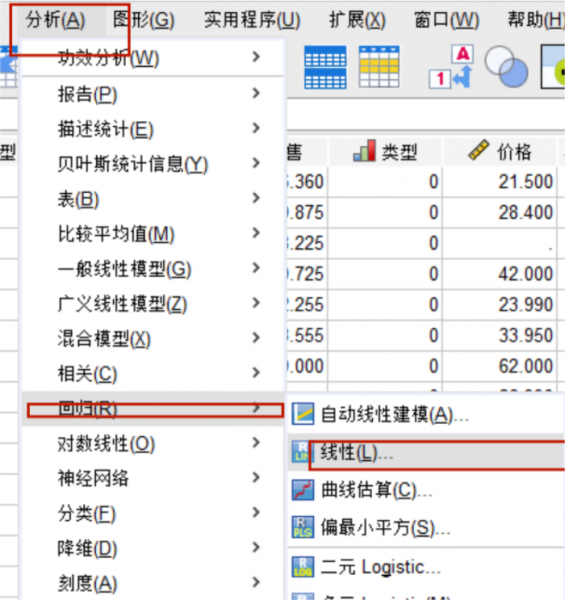
一、spss多元线性回归分析操作步骤
spss多元线性回归分析,用于研究多个自变量与因变量的线性相关关系。本文会以研究客流量、销售量与销售额的线性相关关系为例,演示一下spss多元线性回归方程的分析过程。
本例使用的数据如图1所示,客流量、销售量作为自变量,销售额作为因变量。
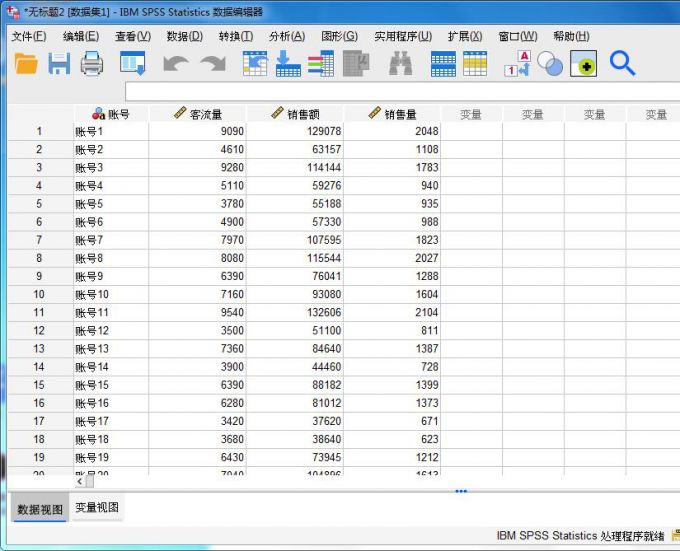
图1:销售额与客流量数据 依次单击spss的回归-线性分析,多元线性与一元线性回归相似,都是使用线性回归分析,只是在自变量的设置上,多元线性回归分析会包含多个自变量,而一元线性回归只会包含一个自变量。
图2:线性回归 变量设置,将客流量、销售量设置为自变量,将销售额设置因变量,以研究客流量、销售量与销售额之间的回归关系。
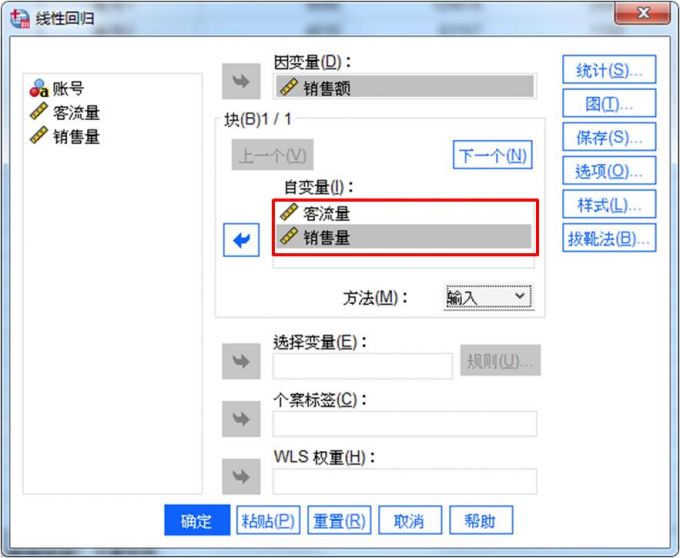
图3:变量设置 设定统计量以计算回归方程的系数,检验系数的显著性以方程的拟合优度,以检验方程的预测准确度,可勾选以下统计量:
1. 勾选回归系数中的“估算值”并设定为95%置信区间,用于检验回归系数的显著性。
2.勾选“模型拟合”,检验回归模型的拟合优度,以确认方程的预测准确性。
3. 勾选“描述”统计量,了解数据的基本特征,如平均值、方差等,查看数据的离散程度。
图4:统计量 图表设定,勾选“直方图”与“正态概率图”,了解回归方程的残差数据分布,以检验残差是否服从正态分布,以满足回归分析的假设。
图5:图表 二、spss多元线性回归分析结果解读
完成以上设置后,进行spss的运算并解读结果。
首先,先观察回归方程的残差直方图(残差的分布),可观察到残差服从正态分布,满足了线性回归模型的对于残差正态性的要求。
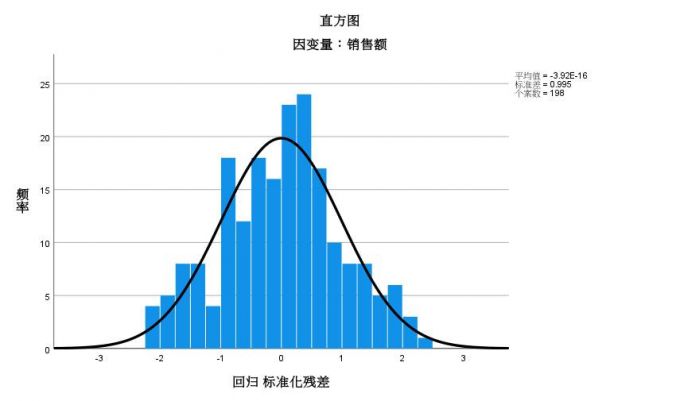
图6:标准化残差直方图 正态P-P图,预期累积概率与实测累积概率的分布趋近于一条直线,同样说明了回归方程的残差服从正态分布。
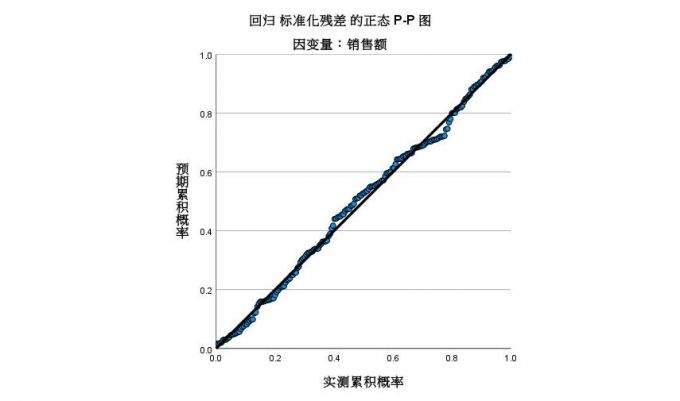
图7:正态P-P图 在满足残差正态分布的前提下,检验模型的拟合优度,模型的调整后R方数值为0.976,接近于1,说明模型的拟合优度高。
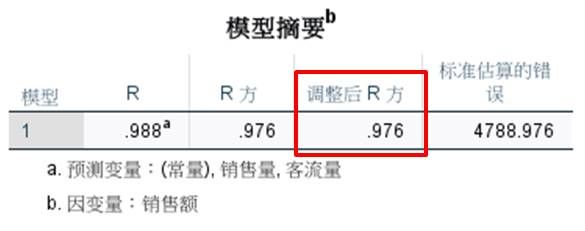
图8:模型拟合优度 在满足残差正态性分布、回归模型拟合优度高的前提下,观察所得回归方程的回归系数的显著性。
从系数分析表看到,回归方程的客流量与销售量系数为<0.001,小于0.05,有95%的概率拒绝原假设,说明客流量与销售量的回归系数均显著,但常量系数0.179>0.05,常量回归系数不显著,说明其数值对回归方程的影响意义不大。
根据以上系数检验结果列出以下方程:y=1.74x1+53.265x2
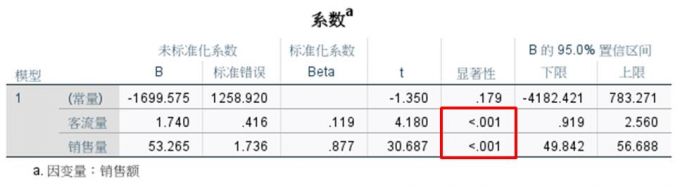
图9:系数显著性 三、怎么判断变量间是否存在线性关系
通过以上的讲述,我们知道怎么运用spss进行多元线性回归分析,但需要确认数据满足线性分布才能进行多元回归分析。那么,在进行运算前,怎么确认数据变量间是否存在线性关系?
最简单的方法是运用散点图观察数据的分布,以确认变量间是否存在线性关系。以一组简单的客流量与销售额数据为例。
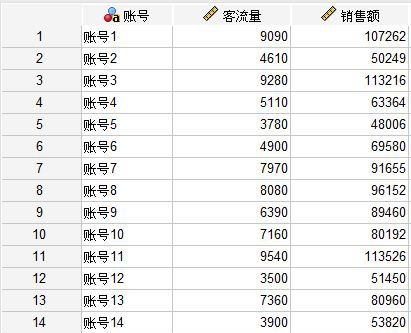
图10:销售额与客流量数据 使用以上数据绘制散点图(可在spss的图表功能中绘制),如图11所示,可以看到,销售额与客流量的数据呈现线性分布,趋势比较明显,说明该组数据可构建线性回归模型进行分析。
如果在散点图中,变量的分布不符合线性分布,就需要使用spss的其他非线性回归分析方法,不能简单套用以上线性回归操作。
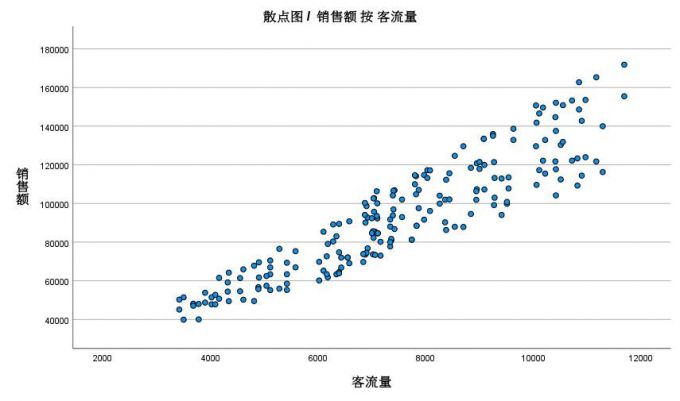
图11:销售额与客流量散点图 四、小结
以上就是关于spss多元线性回归分析操作步骤,spss多元线性回归分析结果解读的相关内容。spss多元线性回归是在一元线性回归的基础上,构建多个自变量的线性回归方程,需要满足残差正态分布的假设,进行方程拟合优度、回归系数显著性的检验。
作者:泽洋
展开阅读全文
︾
标签:SPSS,IBM SPSS Statistics,一元线性回归分析,SPSS教程,多元线性,SPSS分析数据,多元线性回归分析SPSS,多元线性回归分析
读者也访问过这里:热门文章SPSS数据分析显著性差异分析步骤 SPSS显著性差异分析结果怎么看数据的显著性差异分析主要有三种方法,分别是卡方检验、T检验和方差分析。这三种方法都有具体的数据要求:卡方检验是对多个类别的数据进行分析,T检验是对两组数据进行分析,方差分析是对多组数据进行检验。下面,小编具体说明一下SPSS数据分析显著性差异分析步骤,SPSS显著性差异分析结果怎么看。2022-01-07实践SPSS单因素方差分析之检验结果解读在《实践SPSS单因素方差分析之变量与检验方法设置》一文中,我们已经详细地演示了IBM SPSS Statistics单因素方差分析方法的变量选择以及相关的选项、对比设置。2021-01-11spss如何做显著性分析 spss显著性差异分析怎么标abc在统计分析中,显著性分析是分析相关因素之间是否存在显著影响关系的关键性指标,通过它可以说明分析结论是否由抽样误差引起还是实际相关的,可论证分析结果的准确性。下面大家一起来看看用spss如何做显著性分析,spss显著性差异分析怎么标abc。2022-03-14SPSS回归分析中的f值是什么 SPSS回归分析F值在什么范围合适回归分析中以R表示相关性程度的高低,以F评价回归分析是否有统计学的意义,使用IBM SPSS Statistics进行回归分析,可以非常快速的完成R,F的计算,并且给出回归曲线方程,那么,SPSS回归分析中f值是什么?SPSS回归分析F值在什么范围合适,本文结合实例向大家作简单的说明。2022-07-22SPSS多元logistic回归分析的使用技巧回归分析是数据处理中较为常用的一类方法,它可以找出数据变量之间的未知关系,得到较为符合变量关系的数学表达式,以帮助用户完成数据分析。2021-04-26SPSS相关性分析结果怎么看相关性分析是对变量或个案之间相关度的测量,在SPSS中可以选择三种方法来进行相关性分析:双变量、偏相关和距离。2021-04-23最新文章SPSS为什么没有事后检验 SPSS事后检验结果怎么看SPSS作为一款优秀的数据统计分析软件,深受数据统计分析人员的喜爱。SPSS之所以这么受欢迎,除了SPSS有很多的数据统计分析方法,可以帮助统计分析人员更高效的进行数据分析,还因为SPSS的人性化操作,一些刚入行的统计小白,也可以快速的掌握SPSS,接下来给大家详细介绍有关SPSS为什么没有事后检验,SPSS事后检验结果怎么看的相关内容。2026-01-30SPSS重复测量怎样分析 SPSS重复测量球形性应如何检验重复测量是数据分析中的一个重要环节。主要用来分析和检验数据样本中同一对象的相同指标在不同条件或者环境之下的变化情况,所以需要对这部分数据进行重复的测量和分析。例如我们统计一组大学生毕业后的就业情况,那么大学生的专业分类和性别都一致的情况下,就需要分析不同的就业影响因素对于最后就业率的影响。下面给大家介绍SPSS重复测量应当怎样分析,SPSS重复测量球形性应如何检验。2026-01-14SPSS亚组分析的注意事项 SPSS亚组分析结果解读对于经常与数据分析打交道的小伙伴来说,想必对亚组分析这个概念应该不会感到陌生。亚组分析是用来检测异质性结果的方法之一,亚组分析的数据结果分为确证性、支持性和探索性三类。而我们在进行亚组分析时,可以借助数据分析软件SPSS的帮助,它一方面可以帮助我们得到亚组分析的数据结果,还能够把这些数据分析结果以报告形成呈现出来。接下来给大家介绍SPSS亚组分析的注意事项, SPSS亚组分析结果解读的具体内容。2026-01-14SPSS卡方检验样本不满足要求怎么办 卡方检验SPSS结果都小于0.5说明了什么在数据分析的过程中,卡方样本检验是常见的一种统计方式。卡方检验主要用来检验数据样本之间的离散程度,进而判断不同数据之间的偏差值,如果数据样本在统计的时候不符合实际的统计需求,就可能导致卡方检验不满足要求。所以我们需要在统计的过程中对数据样本和统计方法进行调整,这样能够规避数据样本检验带来的结果偏差风险。下面以SPSS为例,给大家介绍SPSS卡方检验样本不满足要求怎么办,卡方检验SPSS结果都小于0.5说明了什么的具体内容。2026-01-14SPSS事后比较怎样进行 SPSS事后比较多重校正应如何设置在数据分析的过程中,经常会在数据分析之后对它进行事后比较的操作。事后比较可以在方差分析的基础之上帮助我们快速找到具体存在差异的数据组。简单来说,大家可以把方差分析理解为起到了一个提示作用,告诉了我们数据样本中的均值并不相等且存在差异,但是如果想要找到具体的差异点在哪里,就需要用到事后比较了。而在进行事后比较的过程中,还会遇到设置多重校正的情况。下面以SPSS为例,给大家介绍SPSS事后比较怎样进行,SPSS事后比较多重校正应如何设置。2026-01-14SPSS怎么查看缺失值分布 SPSS数据缺失严重怎么处理更合理我们在对数据样本进行统计时,经常会遇到排查缺失值的情况,缺失值指数据样本分析中出现的数值丢失情况。如果数据样本中存在的缺失值数量较多的情况,可能会导致数据分析的结果出现偏差。SPSS作为一款专业的数据分析软件,许多用户都会用它来进行数据分析,下面我们以SPSS为例,向大家介绍SPSS怎么查看缺失值分布,SPSS数据缺失严重怎么处理更合理的具体内容。2026-01-14微信公众号
欢迎加入 SPSS 产品的大家庭,立即扫码关注,获取更多软件动态和资源福利。
读者也喜欢这些内容:
-
SPSS怎么做多元线性回归 SPSS共线性诊断怎么判断严重性
高考总分的构成是多元线性关系的一个典型例子,具体可表现为“总分=语文+数学+英语+...”。在这个关系中,总分是因变量,语文、数学和英语等科目是自变量,因变量会随着各个自变量的变化而变化。那么假设存在一个因变量y,受到自变量x1、x2和x3的影响,但是我们并不知道具体是如何变化的,我们该如何判断他们之间的关系呢?这时候就需要多元线性回归出场了,多元线性回归就是一种研究一个因变量与多个自变量之间线性关系的数学方法。本文中我就以SPSS软件为例,回答大家关于“SPSS怎么做多元线性回归,SPSS共线性诊断怎么判断严重性”的问题。...
阅读全文 >
-
SPSS显著性小于0.001的意义 SPSS显著性大于0.05怎么办
在使用SPSS软件进行数据分析工作的过程中,得到的显著性水平分析结果具有极为重要的作用。它能够帮助我们衡量变量之间是否存在真实的关联,或者不同组别数据之间是否存在实质性的差异。今天我们就一起来探讨关于SPSS显著性小于0.001的意义,SPSS显著性大于0.05怎么办的问题。...
阅读全文 >
-
SPSS如何计算z-score SPSS做z-score标准化
作为综合性的数字分析工具,SPSS不仅可以实现数值计算和比对的功能,还能够帮助研究者检验和提取出异常数值,也就是SPSS的检验功能,例如z-score的方法可以将所有数据转化为标准化数据,再依据z值标准筛选出异常数值。本文以SPSS如何计算z-score,SPSS做z-score标准化这两个问题为例,简单介绍一下SPSS的z-score方法如何操作。...
阅读全文 >
-

SPSS变量名称怎么改,SPSS变量名称非法字符怎么办
变量是我们进行数据分析的主体,变量的类型和名称有很多,我们需要为不同的变量设定不同的名称,才能使SPSS有效地识别并判断出它们之间的数据属性。今天我就以SPSS变量名称怎么改,SPSS变量名称非法字符怎么办这两个问题为例,来向大家讲解一下SPSS中有关变量名称设定的相关知识。...
阅读全文 >
-





