


- 首页
- 产品
- 下载
-
帮助中心
SPSS主成分分析特征向量在哪 SPSS主成分分析法的结果怎么解读
发布时间:2022-06-06 10: 49: 56
品牌型号:Dell N5010
系统:Windows 10
软件版本:IBM SPSS Statistics试用版
主成分分析(Principal Component Analysis,PCA)以降维方式,在尽量损失较少信息的前提下,通过正交变换,将一组可能存在相关性的多个变量转换为一组线性不相关的少数变量,转换生成的综合指标称之为主成分。主成分载荷矩阵,或者称为主成分特征向量,可以由因子载荷矩阵计算得出。借助IBM SPSS Statistics,我们可以非常方便完成主成分分析,SPSS主成分分析特征向量在哪?SPSS主成分分析法的结果怎么解读,本文将向大家做简单介绍。
一、SPSS主成分分析特征向量在哪
主成分分析特征向量不能直接给出,需要进行计算,我们以一组数据为例,进行主成分分析,分析结果及分析过程我们会分别在第二第三小节中进行介绍。
我们首先计算主成分分析特征向量。复制成分矩阵数据到数据表中,并将三个向量命名为A1,A2,A3。
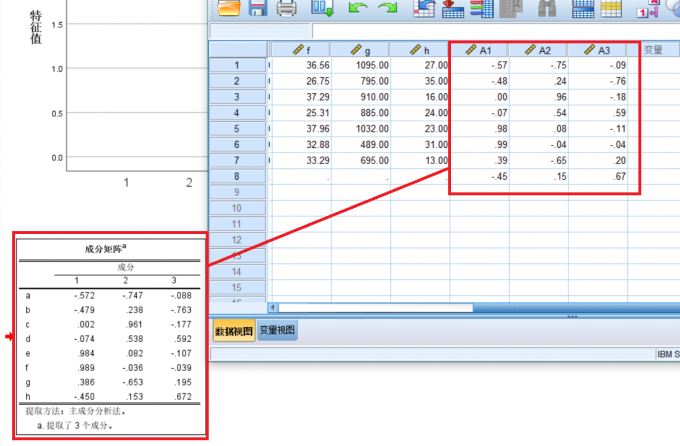
图1复制成分矩阵到数据表中 主成分特征向量计算公式为U=A/sqrt(λ),我们已知A,λ在分析结果的总方差解释表中,A1,A2,A3对应的特征值分别为2.861,2.285,1.475,我们点击转换,计算变量,输入目标变量U的名称,将A1加入数字表达式,然后按公式录入λ平方根,点击确定,SPSS将自动进行向量计算。同样方法计算U2,U3。

图2 计算特征向量U 计算完毕后,我们在数据表中得出特征向量组U1,U2,U3。
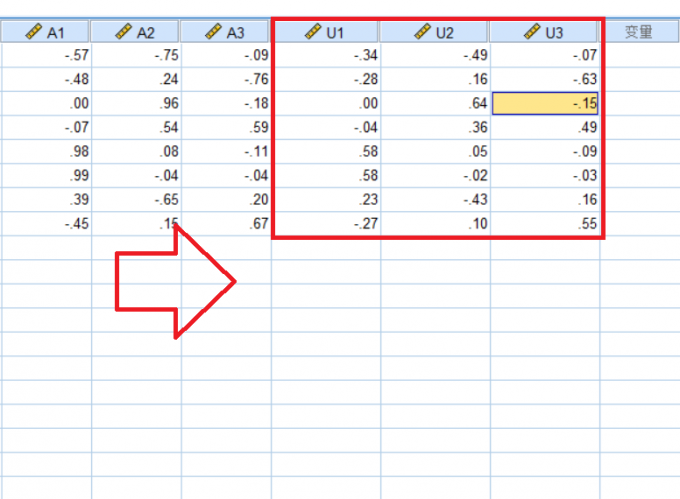
图3 特征向量组U1,U2,U3 U1,U2,U3组成的矩阵就是该问题主成分分析的特征矩阵,该特征矩阵左乘目标数据集,即可得到一组主成分变量。
二、SPSS主成分分析法的结果怎么解读
首先我们观察总方差解释,提取的三个主成分累计为82.761,说明此三个变量就能较好的解释结果,可以用此三个变量代替总共的八个变量。
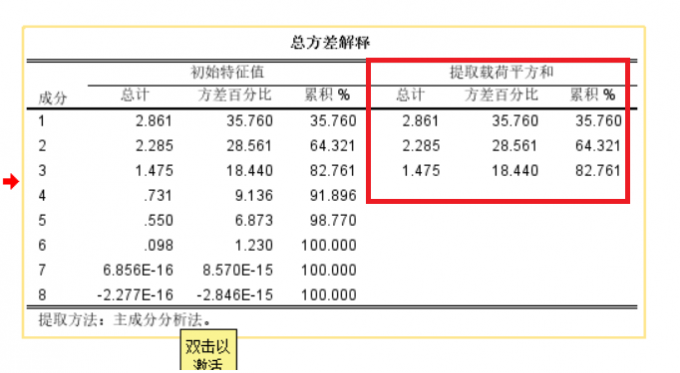
图4 总方差解释 然后我们查看碎石图,在第四个组件时曲线递减速率发生变化,佐证了上述的结论,三个变量就可以解释结果。
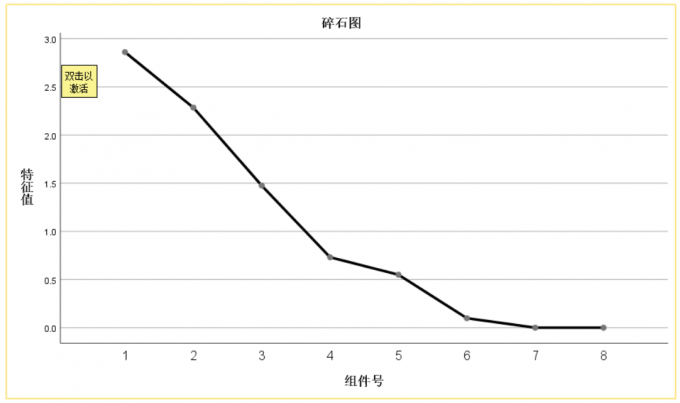
图5 碎石图 我们在成分矩阵可以看出,e,f在第一组向量中影响较高,c在第二组向量中影响较高,d和h在第三组向量中影响较大。

图6 成分矩阵 综合以上分析,第一小节中得出的主成分矩阵以及主成分变量可以很好的解释当前问题,原有的8个变量可以减少至3个。
三、SPSS主成分分析步骤
录入数据后,点击分析,降维,因子,进入主成分分析界面。
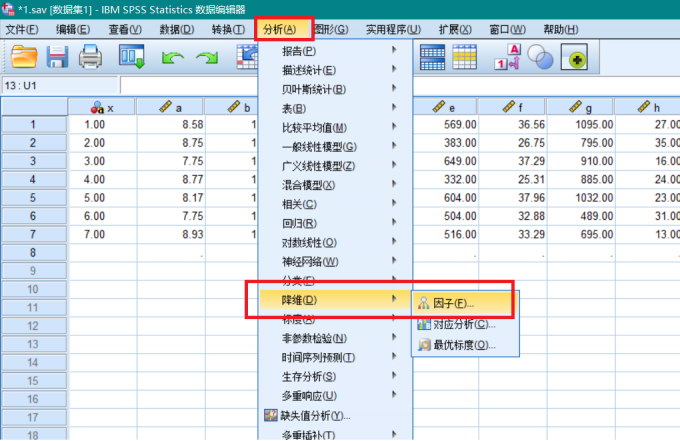
图7 降维进行因子分析 将数据加入变量列表,点击描述,勾选初始解,系数,KMO检验选项。然后点击继续。
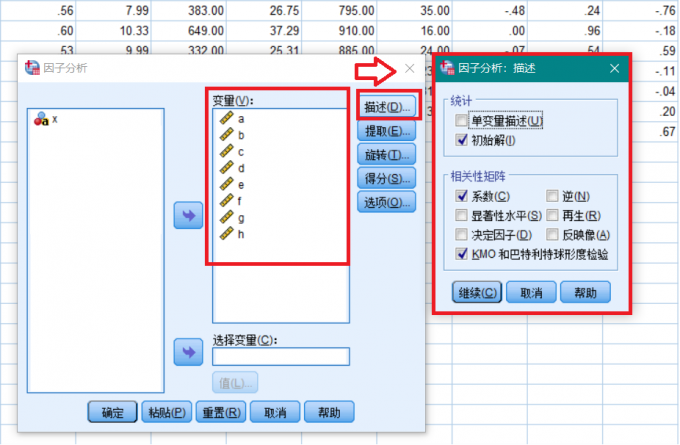
图8 因子分析描述设置 点击提取,勾选相关性矩阵,未旋转因子解,碎石图,点击继续。点击确定,SPSS将对数据进行主成分分析。
由于主成分特征向量需要进行计算,SPSS并不会直接显示,所以很多用户会有SPSS主成分分析特征向量在哪这样的疑问,本文向大家介绍了主成分特征矩阵的计算方法,大家可以参考,SPSS主成分分析法结果怎么解读?我们只要找到平方和载荷累计高于80%的几组主成分,构建主成分向量特征矩阵即可。
作者:莱阳黎曼
展开阅读全文
︾
标签:SPSS,IBM SPSS Statistics,SPSS教程,主成分分析,SPSS主成分分析,SPSS主成分分析法,SPSS主成分分析步骤
读者也访问过这里:热门文章SPSS数据分析显著性差异分析步骤 SPSS显著性差异分析结果怎么看数据的显著性差异分析主要有三种方法,分别是卡方检验、T检验和方差分析。这三种方法都有具体的数据要求:卡方检验是对多个类别的数据进行分析,T检验是对两组数据进行分析,方差分析是对多组数据进行检验。下面,小编具体说明一下SPSS数据分析显著性差异分析步骤,SPSS显著性差异分析结果怎么看。2022-01-07实践SPSS单因素方差分析之检验结果解读在《实践SPSS单因素方差分析之变量与检验方法设置》一文中,我们已经详细地演示了IBM SPSS Statistics单因素方差分析方法的变量选择以及相关的选项、对比设置。2021-01-11spss如何做显著性分析 spss显著性差异分析怎么标abc在统计分析中,显著性分析是分析相关因素之间是否存在显著影响关系的关键性指标,通过它可以说明分析结论是否由抽样误差引起还是实际相关的,可论证分析结果的准确性。下面大家一起来看看用spss如何做显著性分析,spss显著性差异分析怎么标abc。2022-03-14SPSS回归分析中的f值是什么 SPSS回归分析F值在什么范围合适回归分析中以R表示相关性程度的高低,以F评价回归分析是否有统计学的意义,使用IBM SPSS Statistics进行回归分析,可以非常快速的完成R,F的计算,并且给出回归曲线方程,那么,SPSS回归分析中f值是什么?SPSS回归分析F值在什么范围合适,本文结合实例向大家作简单的说明。2022-07-22SPSS多元logistic回归分析的使用技巧回归分析是数据处理中较为常用的一类方法,它可以找出数据变量之间的未知关系,得到较为符合变量关系的数学表达式,以帮助用户完成数据分析。2021-04-26SPSS相关性分析结果怎么看相关性分析是对变量或个案之间相关度的测量,在SPSS中可以选择三种方法来进行相关性分析:双变量、偏相关和距离。2021-04-23最新文章SPSS非参数检验怎么测中位数 SPSS非参数检验z值的意义IBM SPSS Statistics这款软件对用户非常友好,例如非参数检验、数据随机性验证等统计分析,不需要复杂的操作,跟着步骤提示进行操作,即可快速生成统计结果表,新手也能快速掌握。今天我们就围绕SPSS非参数检验怎么测中位数,SPSS非参数检验z值的意义相关内容为大家展开介绍。2026-01-30SPSS随机值检验步骤 SPSS随机检验结果怎么看很多人都听过IBM SPSS Statistics这款软件,它是数据分析的可靠搭档,不仅能轻松搞定数据的整理、转换,最后还能自动生成图表,对新手非常友好。对于经常需要进行学术研究、市场调研的用户来说是个常用的选择。今天我们就来说一下SPSS随机值检验步骤,SPSS随机检验结果怎么看的相关内容。2026-01-30SPSS为什么没有事后检验 SPSS事后检验结果怎么看SPSS作为一款优秀的数据统计分析软件,深受数据统计分析人员的喜爱。SPSS之所以这么受欢迎,除了SPSS有很多的数据统计分析方法,可以帮助统计分析人员更高效的进行数据分析,还因为SPSS的人性化操作,一些刚入行的统计小白,也可以快速的掌握SPSS,接下来给大家详细介绍有关SPSS为什么没有事后检验,SPSS事后检验结果怎么看的相关内容。2026-01-30SPSS重复测量怎样分析 SPSS重复测量球形性应如何检验重复测量是数据分析中的一个重要环节。主要用来分析和检验数据样本中同一对象的相同指标在不同条件或者环境之下的变化情况,所以需要对这部分数据进行重复的测量和分析。例如我们统计一组大学生毕业后的就业情况,那么大学生的专业分类和性别都一致的情况下,就需要分析不同的就业影响因素对于最后就业率的影响。下面给大家介绍SPSS重复测量应当怎样分析,SPSS重复测量球形性应如何检验。2026-01-14SPSS亚组分析的注意事项 SPSS亚组分析结果解读对于经常与数据分析打交道的小伙伴来说,想必对亚组分析这个概念应该不会感到陌生。亚组分析是用来检测异质性结果的方法之一,亚组分析的数据结果分为确证性、支持性和探索性三类。而我们在进行亚组分析时,可以借助数据分析软件SPSS的帮助,它一方面可以帮助我们得到亚组分析的数据结果,还能够把这些数据分析结果以报告形成呈现出来。接下来给大家介绍SPSS亚组分析的注意事项, SPSS亚组分析结果解读的具体内容。2026-01-14SPSS卡方检验样本不满足要求怎么办 卡方检验SPSS结果都小于0.5说明了什么在数据分析的过程中,卡方样本检验是常见的一种统计方式。卡方检验主要用来检验数据样本之间的离散程度,进而判断不同数据之间的偏差值,如果数据样本在统计的时候不符合实际的统计需求,就可能导致卡方检验不满足要求。所以我们需要在统计的过程中对数据样本和统计方法进行调整,这样能够规避数据样本检验带来的结果偏差风险。下面以SPSS为例,给大家介绍SPSS卡方检验样本不满足要求怎么办,卡方检验SPSS结果都小于0.5说明了什么的具体内容。2026-01-14微信公众号
欢迎加入 SPSS 产品的大家庭,立即扫码关注,获取更多软件动态和资源福利。
读者也喜欢这些内容:
-
SPSS生存曲线数据怎么录入 SPSS怎么做生存曲线
在数据分析的领域中,生存分析一直是一个重要的概念,它在生物医学领域有着广泛的应用。而在SPSS中录入生存曲线数据,是我们进行生存分析的第一步,也是关键的一步,生存曲线的数据与后续的数据分析有着重要的关联。SPSS软件在其中可以帮助我们快速进行数据分析和曲线绘制,接下来给大家介绍SPSS生存曲线数据怎么录入,SPSS怎么做生存曲线的具体内容。...
阅读全文 >
-
SPSS显著性小于0.001的意义 SPSS显著性大于0.05怎么办
在使用SPSS软件进行数据分析工作的过程中,得到的显著性水平分析结果具有极为重要的作用。它能够帮助我们衡量变量之间是否存在真实的关联,或者不同组别数据之间是否存在实质性的差异。今天我们就一起来探讨关于SPSS显著性小于0.001的意义,SPSS显著性大于0.05怎么办的问题。...
阅读全文 >
-

SPSS因子负荷系数表怎么做 SPSS因素负荷是哪个值
在数据分析领域,SPSS因子分析可以从众多变量中提取出少数因子,这种方法一般是通过构建的指标体系计算出因子得分,而知晓因子负荷系数可以帮助研究者优化实验数据,从而实现对繁杂数据的标准化处理。今天,我们以SPSS因子负荷系数表怎么做,SPSS因素负荷是哪个值这两个问题为例,带大家了解一下SPSS因子负荷的相关知识。...
阅读全文 >
-
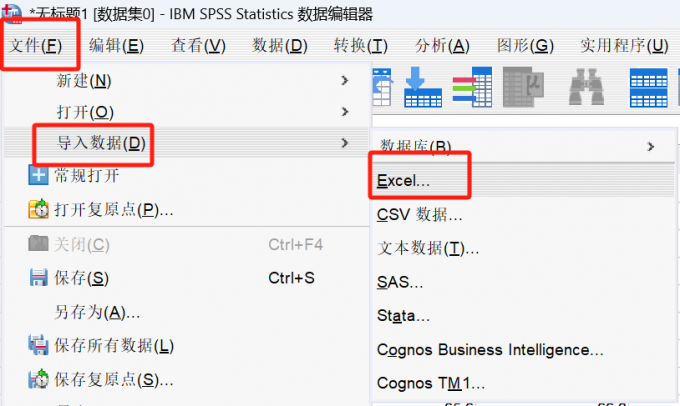
SPSS数据导入是什么意思 SPSS数据导入后显示不完整
在使用SPSS进行数据集分析的时候,可以通过导入数据功能将数据集整体导入到SPSS中,使用起来非常的方便,不过在导入数据集的时候,也会遇到一些问题,例如数据导入不进去、导入进去的数据不完整等等,下面给大家详细讲解有关SPSS数据导入的内容,SPSS数据导入是什么意思,SPSS数据导入后显示不完整。...
阅读全文 >
-





