


- 首页
- 产品
- 下载
-
帮助中心
SPSS线性判别和非线性判别 SPSS线性判别和非线性判别区别
发布时间:2022-06-29 13: 42: 12
品牌型号:Dell N5010
系统:Windows 10
软件版本:IBM SPSS Statistics试用版
判别分析是根据对象属性进行对象分类的一种方法,过程是根据已知对象属性训练出能够判定对象分类的函数,后续输入对象属性后,函数自动对该对象进行判别分类。判别分析通常借助专业的统计分析软件进行,如IBM SPSS Statistics,SPSS线性判别和非线性判别步骤是什么,SPSS线性判别和非线性判别区别是什么,本文简单向大家说明。
一、SPSS线性判别和非线性判别
在SPSS中,我们一般使用的是线性判别,此方法由Fisher提出,开始时是根据iris花的几个形态特点,对150组iris花进行分类。这150组iris花形态数据是非常经典的数据,无论使用软件进行线性判别,或者进行机器学习,都会引用这组数据进行验证。
这里我们仍然以这一组经典数据为例,向大家介绍SPSS线性判别的步骤,首先录入数据如图1所示。其中Species为iris花的种类,已知有三个种类, Sepal.Length, Sepal.Width,Petal.Length,Petal.Width分别为花的形态特点,对应的是测量的统计数据,我们目的在于根据已有的数据,建立合适的判别函数,当我们再遇到一种新的iris花时,我们仅仅需要录入花的形态特点,就能实现自动判别该iris花属于哪个种类。
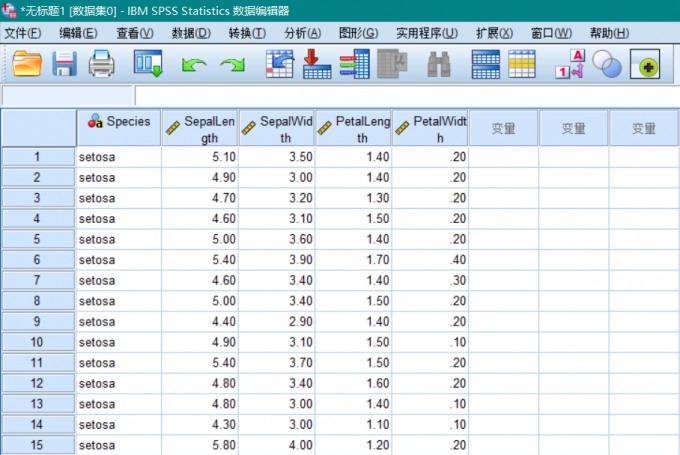
iris花形态分类数据 我们依次点击分析,分类,判别式,如图2所示。

判别式分类 然后将花形态变量录入自变量,将分组号录入分组变量,然后点击定义范围,由于最多有三个组,所以最小值为1,最大值为3。
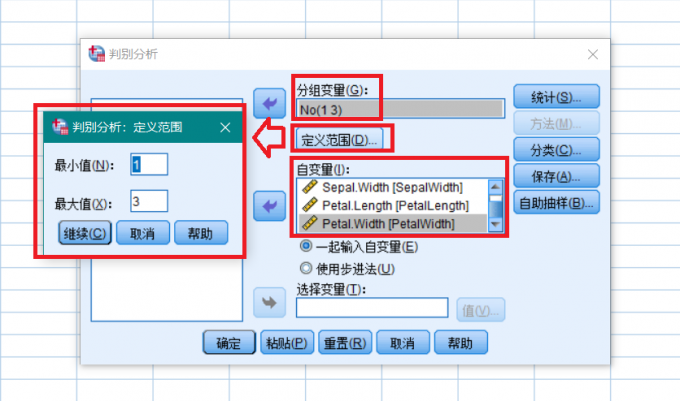
定义分组范围 点击统计,勾选博克斯,未标准化选项,点击继续。
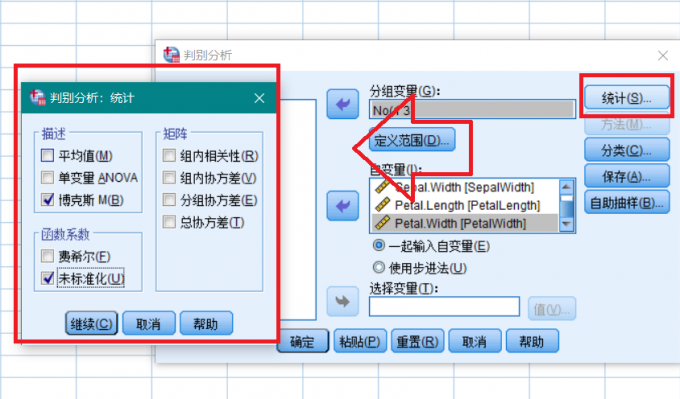
统计选项设置 点击分类,勾选摘要表和合并组选项,点击继续,然后点击确定,SPSS将进行线性判别分析,我们将在第三小节中介绍如何解读判别结果。
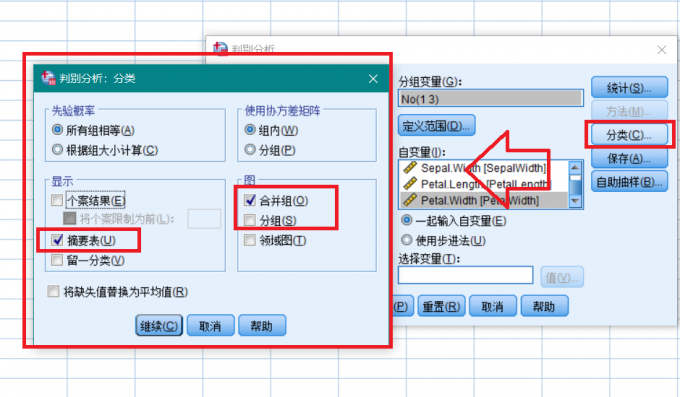
分类选项设置 二、SPSS线性判别和非线性判别区别
对于复杂的分类问题,我们可能会用到非线性判别函数,如下图中,A1,A2,A3为三个集,分布位置比较特别,此时使用线性判别函数无法精确地完成分类工作,直线总会与三个集有交点,借助于分段判别函数和二次判别函数,则可以解决判别问题,这就是线性判别和非线性判别的区别。
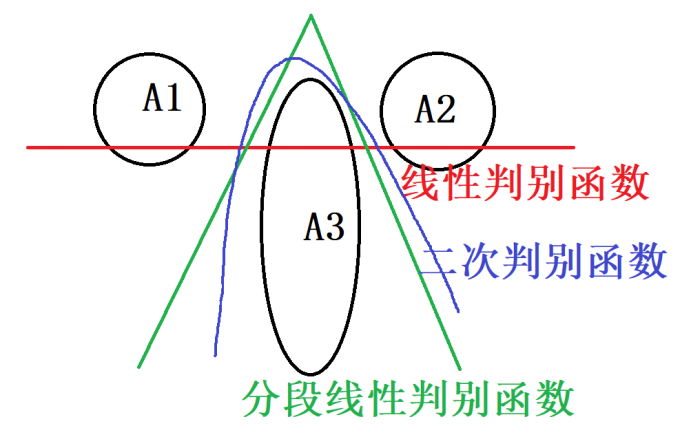
判别函数区别 实际情况下,上述问题非常少见,我们一般借助线性判别就可以解决问题。SPSS中的函数系数也为Fisher线性判别函数。

判别函数系数 三、SPSS线性判别结果解读
首先我们查看分组图,可见第一类setosa和第二类versic,第三类virgin分类较好,第二类和第三类略有重叠。
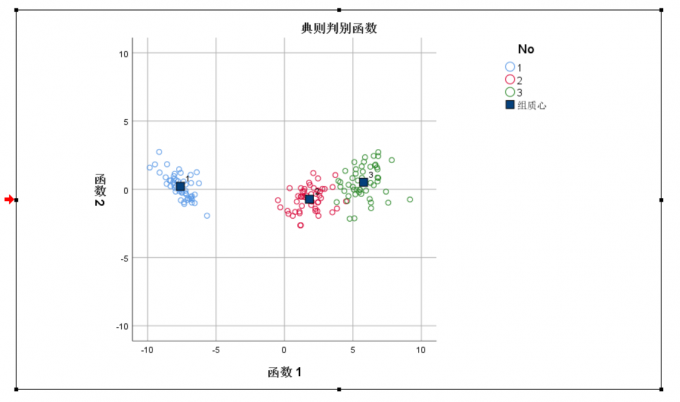
分组图 有了直观认识以后,我们查看分类结果,显示对98%的数据进行了较好的分类,2类和3类略有重叠,结果可以接受。
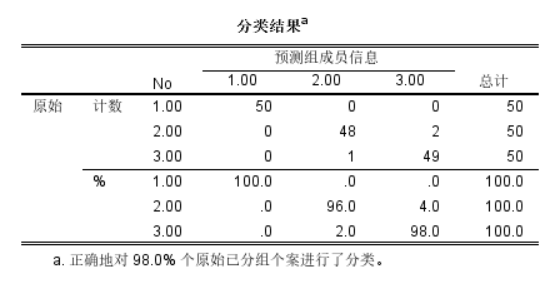
分组结果统计 然后我们查看威尔克Lambda表,判别函数1和判别函数2显著性均小于0.05,有统计学意义。
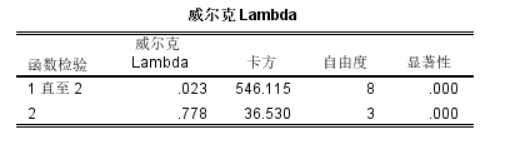
威尔克Lambda表 综合来看,判别函数有统计学意义,分组结果准确性可以接受,Fisher线性判别方法可以很好地解决iris花分类问题。
以上就是SPSS线性判别和非线性判别,SPSS线性判别和非线性判别区别的相关内容了。SPSS线性判别和非线性判别哪个为首选方法,一般首选线性判别,可解决大多数问题,SPSS线性判别和非线性判别在于对于某些集合,使用线性判别可能互有重叠,可借助非线性判别中分段线性和二次判别函数进行。
作者:莱阳黎曼
展开阅读全文
︾
标签:IBM SPSS Statistics,SPSS教程,非线性回归,IBM SPSS
读者也访问过这里:热门文章SPSS数据分析显著性差异分析步骤 SPSS显著性差异分析结果怎么看数据的显著性差异分析主要有三种方法,分别是卡方检验、T检验和方差分析。这三种方法都有具体的数据要求:卡方检验是对多个类别的数据进行分析,T检验是对两组数据进行分析,方差分析是对多组数据进行检验。下面,小编具体说明一下SPSS数据分析显著性差异分析步骤,SPSS显著性差异分析结果怎么看。2022-01-07实践SPSS单因素方差分析之检验结果解读在《实践SPSS单因素方差分析之变量与检验方法设置》一文中,我们已经详细地演示了IBM SPSS Statistics单因素方差分析方法的变量选择以及相关的选项、对比设置。2021-01-11spss如何做显著性分析 spss显著性差异分析怎么标abc在统计分析中,显著性分析是分析相关因素之间是否存在显著影响关系的关键性指标,通过它可以说明分析结论是否由抽样误差引起还是实际相关的,可论证分析结果的准确性。下面大家一起来看看用spss如何做显著性分析,spss显著性差异分析怎么标abc。2022-03-14SPSS回归分析中的f值是什么 SPSS回归分析F值在什么范围合适回归分析中以R表示相关性程度的高低,以F评价回归分析是否有统计学的意义,使用IBM SPSS Statistics进行回归分析,可以非常快速的完成R,F的计算,并且给出回归曲线方程,那么,SPSS回归分析中f值是什么?SPSS回归分析F值在什么范围合适,本文结合实例向大家作简单的说明。2022-07-22SPSS多元logistic回归分析的使用技巧回归分析是数据处理中较为常用的一类方法,它可以找出数据变量之间的未知关系,得到较为符合变量关系的数学表达式,以帮助用户完成数据分析。2021-04-26SPSS相关性分析结果怎么看相关性分析是对变量或个案之间相关度的测量,在SPSS中可以选择三种方法来进行相关性分析:双变量、偏相关和距离。2021-04-23最新文章SPSS重复测量怎样分析 SPSS重复测量球形性应如何检验重复测量是数据分析中的一个重要环节。主要用来分析和检验数据样本中同一对象的相同指标在不同条件或者环境之下的变化情况,所以需要对这部分数据进行重复的测量和分析。例如我们统计一组大学生毕业后的就业情况,那么大学生的专业分类和性别都一致的情况下,就需要分析不同的就业影响因素对于最后就业率的影响。下面给大家介绍SPSS重复测量应当怎样分析,SPSS重复测量球形性应如何检验。2026-01-14SPSS亚组分析的注意事项 SPSS亚组分析结果解读对于经常与数据分析打交道的小伙伴来说,想必对亚组分析这个概念应该不会感到陌生。亚组分析是用来检测异质性结果的方法之一,亚组分析的数据结果分为确证性、支持性和探索性三类。而我们在进行亚组分析时,可以借助数据分析软件SPSS的帮助,它一方面可以帮助我们得到亚组分析的数据结果,还能够把这些数据分析结果以报告形成呈现出来。接下来给大家介绍SPSS亚组分析的注意事项, SPSS亚组分析结果解读的具体内容。2026-01-14SPSS卡方检验样本不满足要求怎么办 卡方检验SPSS结果都小于0.5说明了什么在数据分析的过程中,卡方样本检验是常见的一种统计方式。卡方检验主要用来检验数据样本之间的离散程度,进而判断不同数据之间的偏差值,如果数据样本在统计的时候不符合实际的统计需求,就可能导致卡方检验不满足要求。所以我们需要在统计的过程中对数据样本和统计方法进行调整,这样能够规避数据样本检验带来的结果偏差风险。下面以SPSS为例,给大家介绍SPSS卡方检验样本不满足要求怎么办,卡方检验SPSS结果都小于0.5说明了什么的具体内容。2026-01-14SPSS事后比较怎样进行 SPSS事后比较多重校正应如何设置在数据分析的过程中,经常会在数据分析之后对它进行事后比较的操作。事后比较可以在方差分析的基础之上帮助我们快速找到具体存在差异的数据组。简单来说,大家可以把方差分析理解为起到了一个提示作用,告诉了我们数据样本中的均值并不相等且存在差异,但是如果想要找到具体的差异点在哪里,就需要用到事后比较了。而在进行事后比较的过程中,还会遇到设置多重校正的情况。下面以SPSS为例,给大家介绍SPSS事后比较怎样进行,SPSS事后比较多重校正应如何设置。2026-01-14SPSS怎么查看缺失值分布 SPSS数据缺失严重怎么处理更合理我们在对数据样本进行统计时,经常会遇到排查缺失值的情况,缺失值指数据样本分析中出现的数值丢失情况。如果数据样本中存在的缺失值数量较多的情况,可能会导致数据分析的结果出现偏差。SPSS作为一款专业的数据分析软件,许多用户都会用它来进行数据分析,下面我们以SPSS为例,向大家介绍SPSS怎么查看缺失值分布,SPSS数据缺失严重怎么处理更合理的具体内容。2026-01-14SPSS变量类型怎么修改 SPSS变量标签修改后分析报错怎么办在数据分析这个领域中,我们经常会面临着修改数据变量类型的情况。因为在一组数据变量中会存在着多种不同的变量类型(自变量、因变量、定类变量、定序变量等),这些变量类型在数据样本中担任着不同的角色,在样本分析中也有着不同的作用。下面就以SPSS数据分析软件为例,给大家介绍SPSS变量类型怎么修改,SPSS变量标签修改后分析报错怎么办的具体内容。2026-01-14微信公众号
欢迎加入 SPSS 产品的大家庭,立即扫码关注,获取更多软件动态和资源福利。
读者也喜欢这些内容:
-
SPSS显著性小于0.001的意义 SPSS显著性大于0.05怎么办
在使用SPSS软件进行数据分析工作的过程中,得到的显著性水平分析结果具有极为重要的作用。它能够帮助我们衡量变量之间是否存在真实的关联,或者不同组别数据之间是否存在实质性的差异。今天我们就一起来探讨关于SPSS显著性小于0.001的意义,SPSS显著性大于0.05怎么办的问题。...
阅读全文 >
-
SPSS数据转置什么意思 SPSS数据转置怎么操作
在进行SPSS数据计算和分析之前,研究者通常运用SPSS数据转置的方法,借此对繁杂数据进行行列互换,适用于EXCEL、CSV、文本数据、SAS等各类形式的数据文本,便于研究者清晰全面地了解数据信息。本文以SPSS数据转置什么意思,SPSS数据转置怎么操作这两个问题为例,带大家了解一下SPSS数据转置的相关知识。...
阅读全文 >
-
SPSS数据可视化参数优化 SPSS交互图表制作方法
在数据分析方面,条形图是SPSS数据可视化呈现的重要手段,例如交互作用主题的条形图绘制,不仅可以使研究者直观看出变量之间的关系和差异,还有助于研究者对实验参数进行改良和优化。今天,我们以SPSS数据可视化参数优化,SPSS交互图表制作方法这两个问题为例,带大家了解一下SPSS数据可视化和交互图制作的相关知识。...
阅读全文 >
-
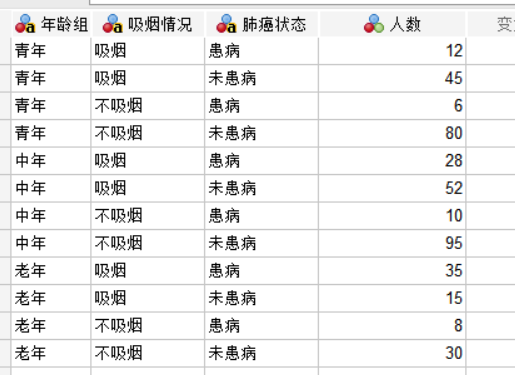
SPSS分层卡方检验步骤 SPSS分层卡方检验结果解读
分层卡方检验是SPSS中常用的统计分析方法之一,常用来识别分类变量中的混杂因素并控制其影响。通过将数据按混杂因素分层后,分别在每一层内分析分类变量之间的关联性,从而排除混杂变量的干扰。接下来本文将来带大家了解SPSS分层卡方检验步骤,SPSS分层卡方检验结果解读的相关内容。...
阅读全文 >
-















