spss回归分析如何操作 spss回归分析的基本步骤

品牌型号：Dell N5010

系统：Windows 10

软件版本：IBM SPSS Statistics

通过回归分析，可以了解变量间是否存在相互依赖的定量关系。根据方程类型，回归分析可以分为线性回归和非线性回归。根据变量的数目多少，回归分析可以分为一元回归分析和多元回归分析。本文以最简单的一元线性回归分析为例向大家介绍SPSS回归分析如何操作，SPSS回归分析的基本步骤。

一、spss回归分析如何操作

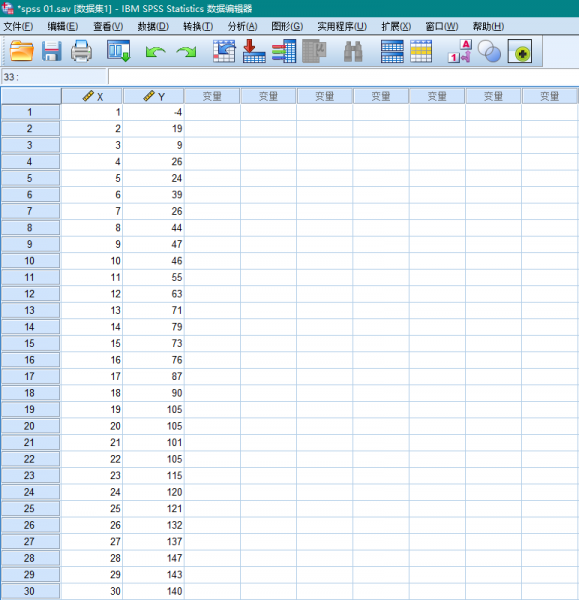
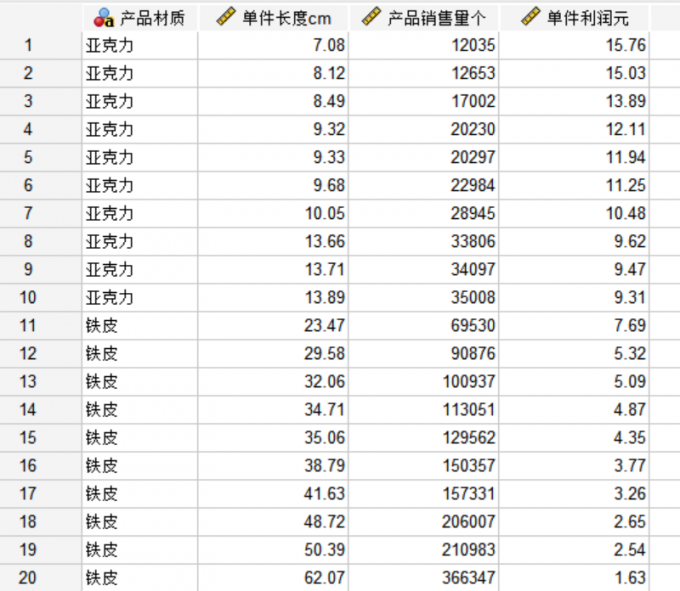
我们以图1中数据为例，向大家介绍如何使用SPSS进行一元线性回归分析。

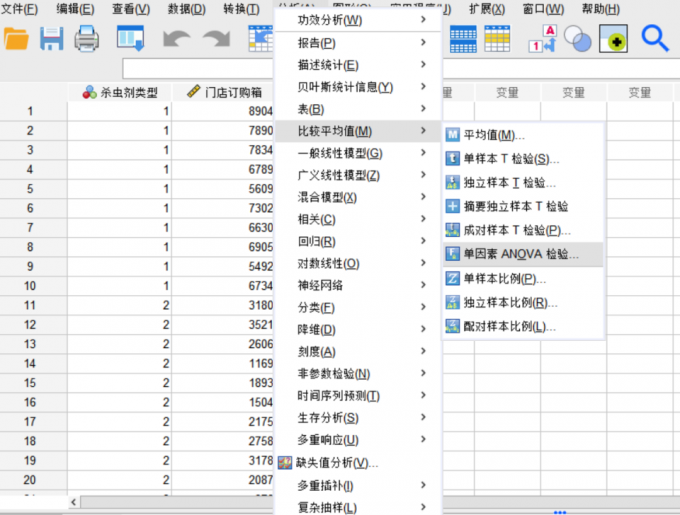
在图2所示界面依次点击【分析】，【回归】，【线性】，进入线性回归分析功能界面。

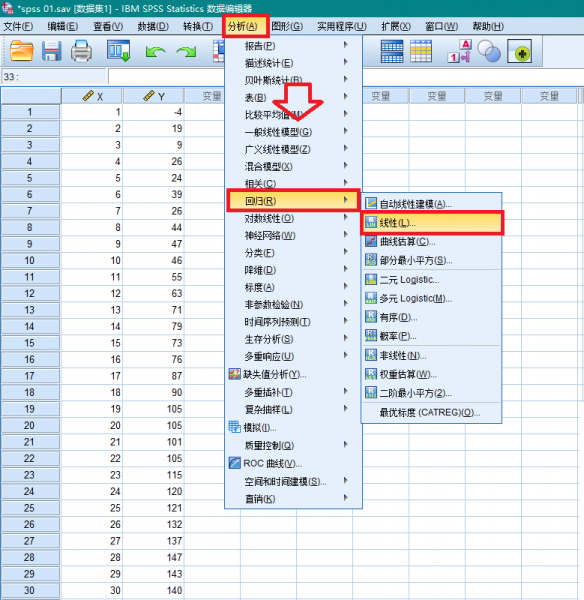
在线性回归分析功能界面，首先将Y指定为因变量，将X指定为自变量，然后点击【统计】按键，在弹出的窗口中，勾选“残差”项目中的“德宾-沃森”和“个案诊断”，点击【继续】。

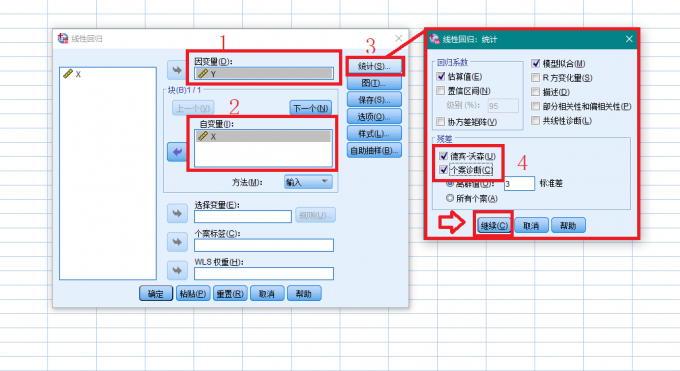
点击【图】按键，将*ZRESID指定为Y，将*ZPRED指定为X，在“标准化残差图”中勾选“直方图”和“正态概率图”，点击【继续】。

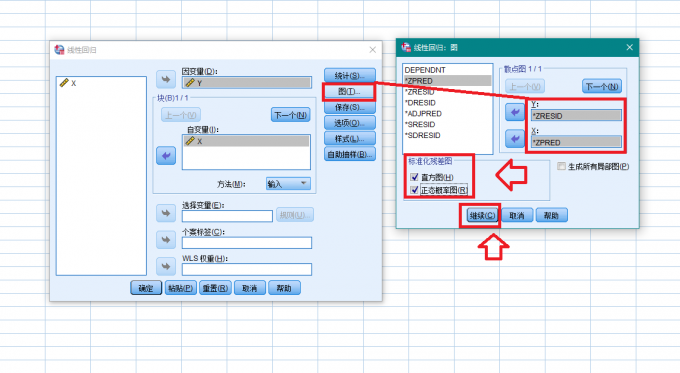
点击【保存】按键，在“距离”选项卡中勾选“库克距离”和“杠杆值”，点击【继续】，点击【确定】。

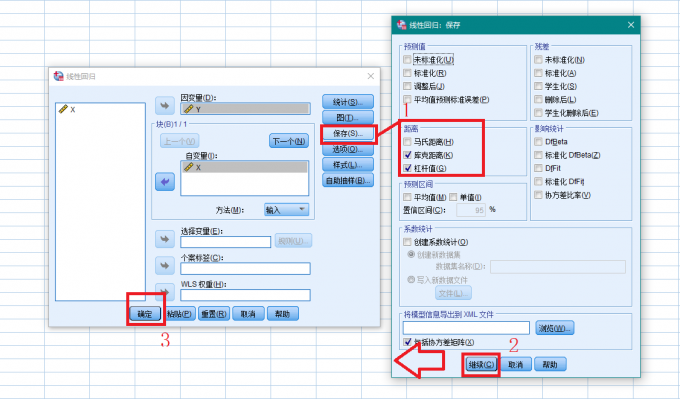
SPSS将对两组数据进行线性回归分析，并将结果输出至查看器，如何对结果进行分析，我们将在第二小节中向大家介绍。

二、spss回归分析的基本步骤

在第一小节中，向大家介绍了使用SPSS进行线性回归分析操作过程，结果应按照什么步骤进行分析，本节继续向大家介绍。

首先查看模型摘要表格，当德宾-沃森统计量为0-2时，存在自相关，德宾-沃森统计量为2-4时，不存在自相关，可以进行线性回归分析，本例中德宾-沃森统计量为2.235，数据不存在自相关。

然后查看残差统计表，库克距离最大值为0.271，小于0.5，提示数据中不存在异常值，符合进行线性回归分析的条件。

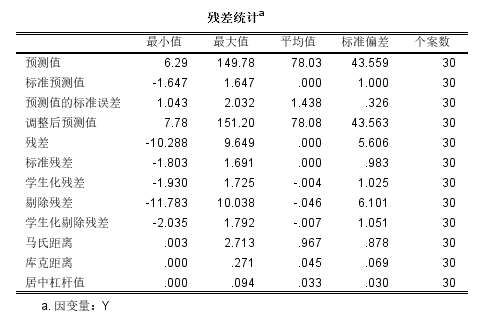
查看P-P图中的数据点是否均匀分布于直线两侧。如果数据点均匀分布于直线两侧，提示数据符合正态分布，满足进行线性回归分析的条件。本例中，数据点均匀分布于直线两侧。

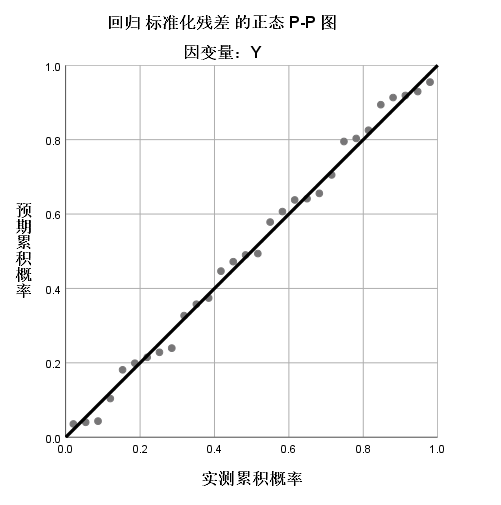
最后进行方差齐性判断，查看散点图中的回归标准化残差是否均匀分布于y=0直线两侧。如果均匀分布，提示方差齐性，可以进行线性回归分析，如果数据点呈扇形或漏斗状分布，则提示方差不齐，不满足进行线性回归分析的条件。

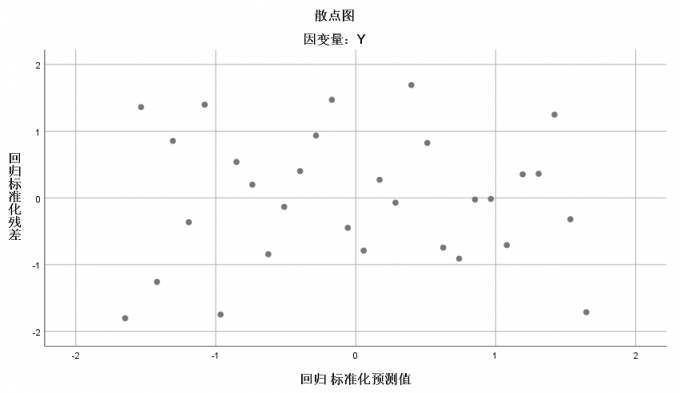
最后查看图9所示的三个表格，首先ANOVA表中回归显著性P为0，提示线性回归分析有统计学意义。然后查看模型摘要表格，R方0.984，提示Y变化的98.4%可以由X解释，线性关系良好。在系数表格中，B（常量）为1.340，BX为4.948，线性回归方程为：Y=4.948*X+1.340。

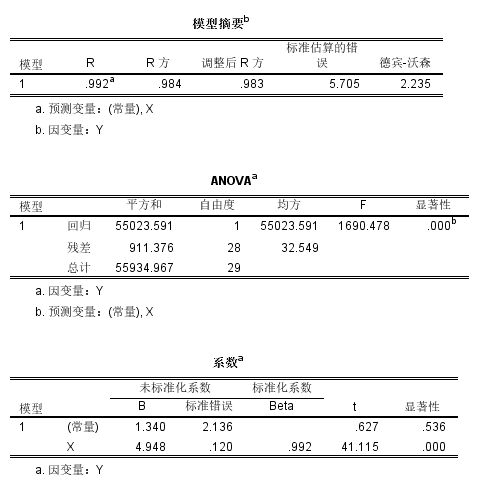
本文分为两个小节，分别向大家介绍了SPSS回归分析如何操作，SPSS回归分析的基本步骤，希望对大家的工作有所帮助。