


- 首页
- 产品
- 下载
-
帮助中心
协方差分析条件不满足 协方差分析的适用条件
发布时间:2022-02-21 14: 13: 05
品牌型号:联想
系统:Win 10
软件版本:IBM SPSS Statistics
关键词:协方差分析,协变量,数据分析
协方差分析在应用的时候,需要满足一定的条件,否则得出的结果不具备参考性。只有核心条件满足时,协方差分析才有参考意义。下面给大家介绍一下协方差分析条件不满足,协方差分析的适用条件的相关解答。
- 协方差分析条件不满足
在实验过程中,会受到干扰因素的影响,这些干扰因素被称为协变量。在进行数据分析时,增添协变量以控制其对实验结果的影响。
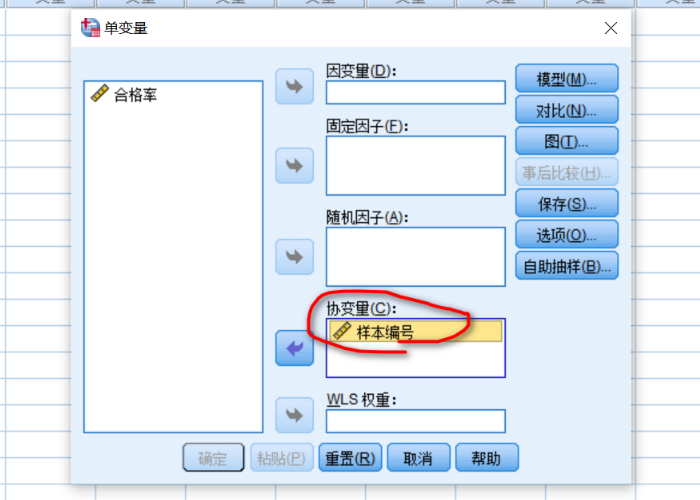
图1:协方差分析 在进行协方差分析之前,实验变量需要满足一定的条件。
- 协变量是连续变量。
- 自变量有2个或两个以上的分组。
- 因变量是连续变量。
- 协变量与因变量之间是线性关系。
- 协变量和因变量的回归直线平行。
- 因变量的残差服从正态分布。
二、协方差分析的适用条件
协方差分析的使用条件有6个,其中1、2、3可以根据数据直接判断出来。4、5、6条件需要进行分析。
具体操作如下:
- 验证协变量与因变量之间是线性关系。
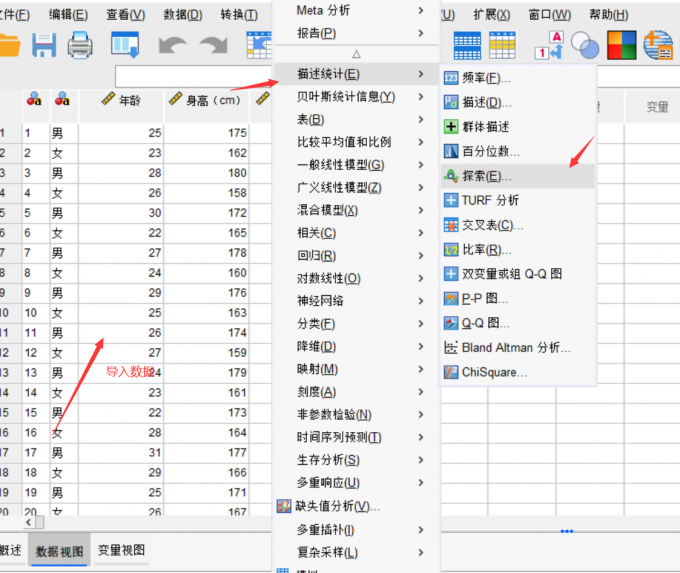
打开SPSS软件,将数据文件导入。
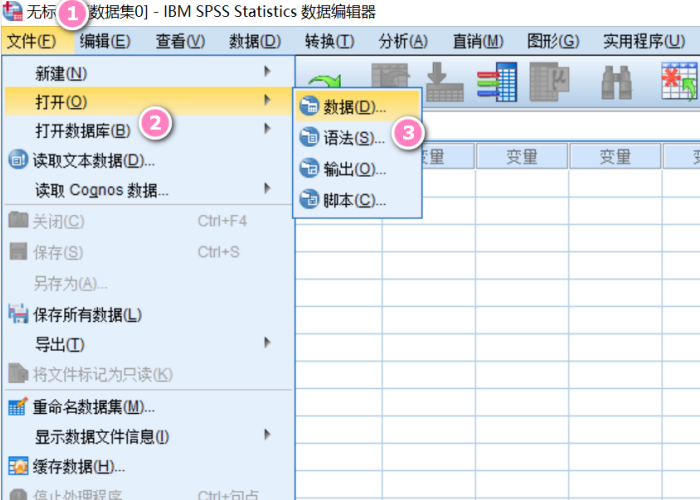
图2:导入文件 首先,根据数据绘制出散点图,由散点图得到拟合曲线,验证协变量和因变量是否是线性关系。鼠标单击“图形”,选择“图表构建器”。随后弹出名为“图表构建器”的设置对话框。
在这个对话框里,选择散点图,双击第二个图标激活。横坐标选择培训前测试成绩,纵坐标选择培训后测试成绩。右上角的方框选择职称。元素属性中,选择纵坐标,将最小值的对勾取消。设置完成单击“确定”。
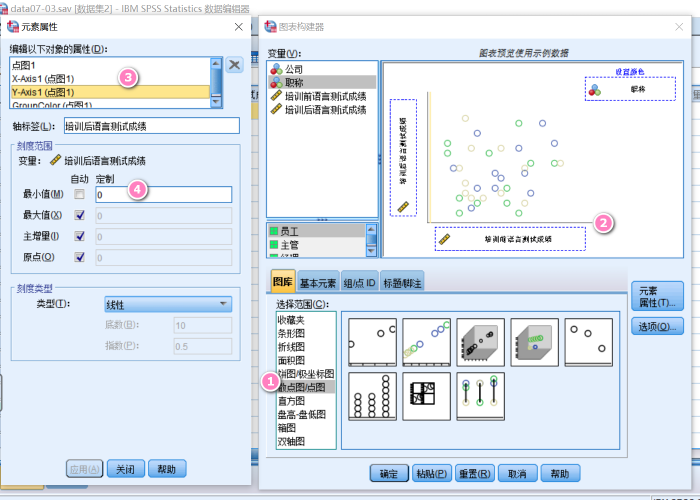
图3:散点图设置 数据分析结束后,会得到散点图,双击散点图将其激活,打开名为图标编辑器的设置对话框。在这里,单击元素,选择子组拟合线,就可以得到协变量和因变量的线性关系图了。证明协变量与因变量存在线性关系。
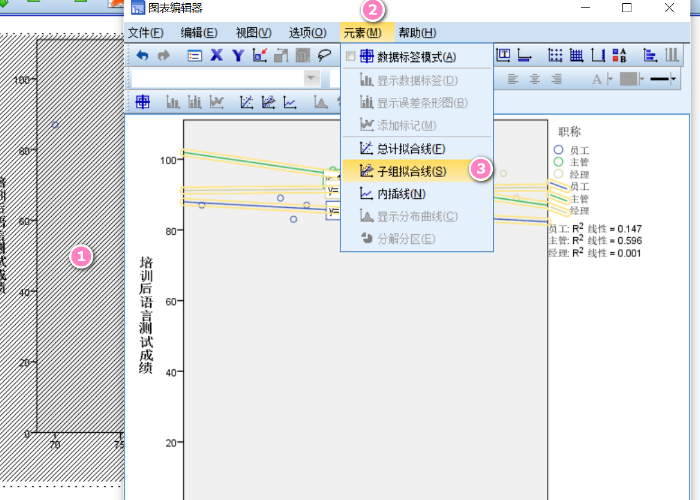
图4:子组拟合线 - 验证协变量和因变量回归直线平行。
单击“分析”,选择“一般线性模型”中的“单变量”。打开名为“单变量”的设置对话框。在因变量中选择培训后语言成绩,固定因子选择职称,协变量选择培训前语言测试成绩。
单击模型选项,打开名为“单变量:模型”的设置对话框,将职称和培训前语言测试成绩导入右边的模型列表中,然后按住shift键,将两者全部选中,一起导入模型中,形成培训前测试成绩和职称的交互选项。设置完毕单击“确定”。
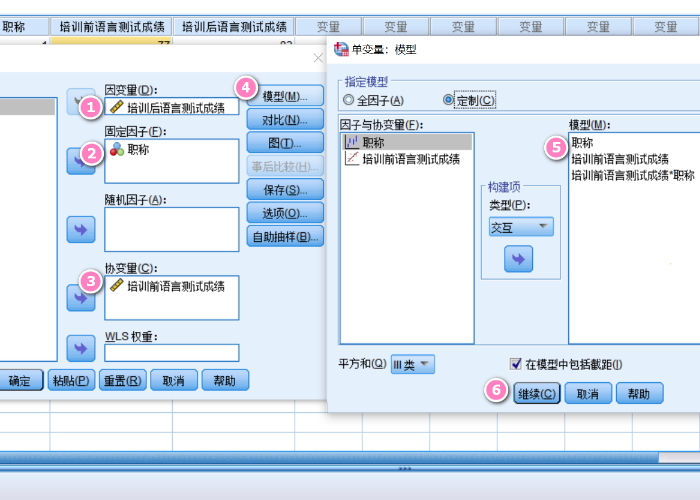
图5:单变量:模型 软件运行后,输出图表。如果自变量与协变量的交互项具有显著性差异,表示各组间回归斜率不同,反之则相同。根据图表数据得知,P值为0.501,大于0.05,不具有显著性差异,说明各组间回归斜率相同。证明协变量与因变量的回归直线平行。
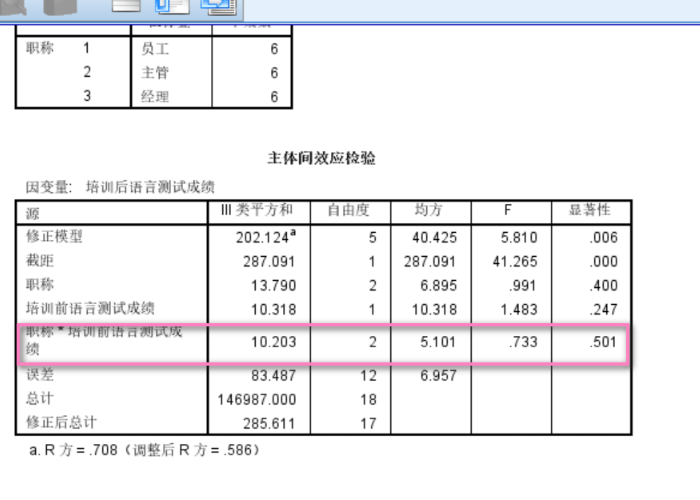
图6:主体间效应检验结果 3、验证因变量的残差服从正态分布。
先根据数据生成预测值和标准化残差。单击“分析”,选择“一般线性模型”中的“单变量”。在弹出的设置对话框中,因变量、固定因子和协变量的选择依然跟上图一样。
单击“模型”,勾选全因子。单击“保存”,勾选为标准化和标准化。单击“选项”,将职称导入右列的估算平均值中,勾选描述统计、齐性检验和效应量估计。设置完毕单击“确定”。软件运行结束后生成PRE_1和ZRE_1。
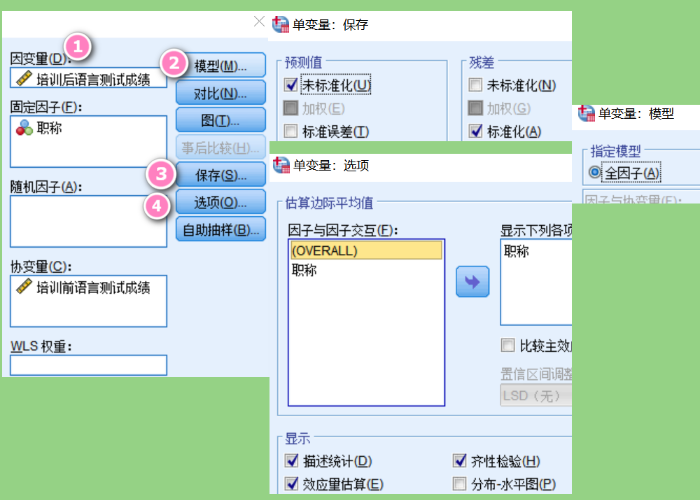
图7:单变量:保存 单击“分析”,选择“描述统计”中的“探索”。因变量选择刚刚生成的ZRE_1,也就是标准化残差。因子列表选择职称。单击“图”的设置按钮,勾选因子级别并置,勾选含检验的正态图。设置完毕单击“确定”。
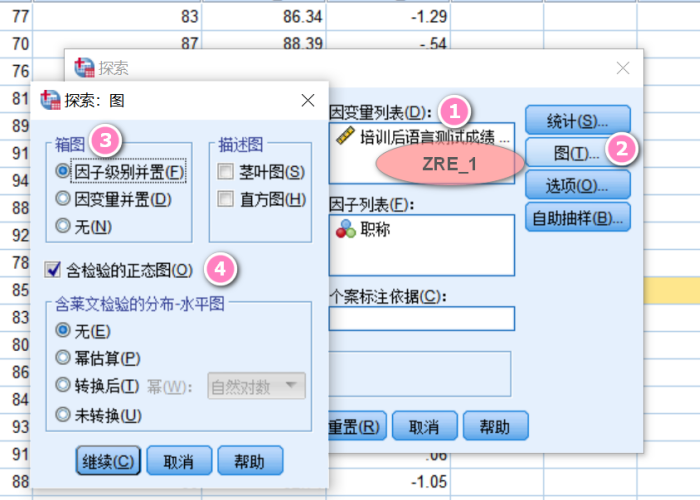
图8:探索:图 软件运行结束后,输出图表。根据表中数据可知,P值均大于0.05,表示数据接近正态分布。证实因变量的残差服从正态分布。
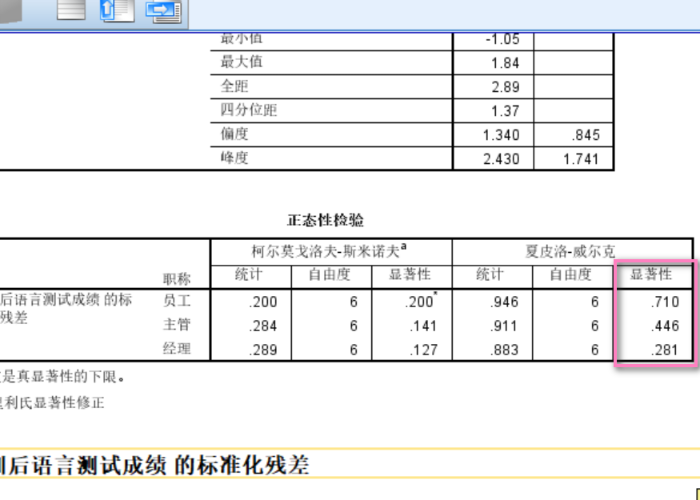
图9:正态检验结果 以上就是协方差分析条件不满足,协方差分析的适用条件的相关解答。如果想要了解更多,可以前往IBM SPSS Statistics官方网站。
作者:小影
展开阅读全文
︾
标签:IBM SPSS Statistics
读者也访问过这里:热门文章SPSS数据分析显著性差异分析步骤 SPSS显著性差异分析结果怎么看数据的显著性差异分析主要有三种方法,分别是卡方检验、T检验和方差分析。这三种方法都有具体的数据要求:卡方检验是对多个类别的数据进行分析,T检验是对两组数据进行分析,方差分析是对多组数据进行检验。下面,小编具体说明一下SPSS数据分析显著性差异分析步骤,SPSS显著性差异分析结果怎么看。2022-01-07实践SPSS单因素方差分析之检验结果解读在《实践SPSS单因素方差分析之变量与检验方法设置》一文中,我们已经详细地演示了IBM SPSS Statistics单因素方差分析方法的变量选择以及相关的选项、对比设置。2021-01-11spss如何做显著性分析 spss显著性差异分析怎么标abc在统计分析中,显著性分析是分析相关因素之间是否存在显著影响关系的关键性指标,通过它可以说明分析结论是否由抽样误差引起还是实际相关的,可论证分析结果的准确性。下面大家一起来看看用spss如何做显著性分析,spss显著性差异分析怎么标abc。2022-03-14SPSS回归分析中的f值是什么 SPSS回归分析F值在什么范围合适回归分析中以R表示相关性程度的高低,以F评价回归分析是否有统计学的意义,使用IBM SPSS Statistics进行回归分析,可以非常快速的完成R,F的计算,并且给出回归曲线方程,那么,SPSS回归分析中f值是什么?SPSS回归分析F值在什么范围合适,本文结合实例向大家作简单的说明。2022-07-22SPSS多元logistic回归分析的使用技巧回归分析是数据处理中较为常用的一类方法,它可以找出数据变量之间的未知关系,得到较为符合变量关系的数学表达式,以帮助用户完成数据分析。2021-04-26SPSS相关性分析结果怎么看相关性分析是对变量或个案之间相关度的测量,在SPSS中可以选择三种方法来进行相关性分析:双变量、偏相关和距离。2021-04-23最新文章SPSS一致性检验数据录入方法 SPSS进行一致性检验怎么做在统计分析中,一致性检验主要用于评估两个评价主体对无序分类变量评价结果的一致性。这种一致性检验适用于很多场景,比如两位医生对病人患病与否的诊断,或是两台机器、两种检验方法对某指标阴性阳性结果的判定等。下面我们一起来探讨关于SPSS一致性检验数据录入方法,SPSS进行一致性检验怎么做的问题。2026-03-03SPSS折线图横坐标方向怎么调整 SPSS折线图横坐标不是变量怎么办在日常的数据分析工作中,我们可以根据折线图里的点位变化,清晰地看出数据的发展趋势,并将这些已有的趋势转化为未来的发展策略。今天我就以SPSS折线图横坐标方向怎么调整,SPSS折线图横坐标不是变量怎么办这两个问题为例,来向大家讲解一下SPSS中调节折线图横坐标的相关操作技巧。2026-03-03SPSS多个自变量拟合怎么做 SPSS多个自变量相关性检验怎么做用过IBM SPSS Statistics软件的用户应该都清楚它的强大,我们可以用它来进行复杂数据分析,比如多个自变量拟合、相关性检验分析等等,而且软件界面相当友好,刚接触的小白也能快速掌握,本期我们就来介绍一下SPSS多个自变量拟合怎么做,SPSS多个自变量相关性检验怎么做的相关内容。2026-01-30SPSS做ks和sw正态性检验步骤 SPSS正态性检验ks和sw怎么看说到IBM SPSS Statistics,大家第一时间想到的可能就是它的专业统计功能。SPSS软件的数据处理与分析功能确实非常不错,很多科研、教育、市场研究等领域的用户都在使用。不过很多新手可能会觉得操作步骤复杂,其实不然。接下来我们就来带大家了解一下SPSS做ks和sw正态性检验步骤,SPSS正态性检验ks和sw怎么看的相关内容。2026-01-30SPSS非参数检验怎么测中位数 SPSS非参数检验z值的意义IBM SPSS Statistics这款软件对用户非常友好,例如非参数检验、数据随机性验证等统计分析,不需要复杂的操作,跟着步骤提示进行操作,即可快速生成统计结果表,新手也能快速掌握。今天我们就围绕SPSS非参数检验怎么测中位数,SPSS非参数检验z值的意义相关内容为大家展开介绍。2026-01-30SPSS随机值检验步骤 SPSS随机检验结果怎么看很多人都听过IBM SPSS Statistics这款软件,它是数据分析的可靠搭档,不仅能轻松搞定数据的整理、转换,最后还能自动生成图表,对新手非常友好。对于经常需要进行学术研究、市场调研的用户来说是个常用的选择。今天我们就来说一下SPSS随机值检验步骤,SPSS随机检验结果怎么看的相关内容。2026-01-30微信公众号
欢迎加入 SPSS 产品的大家庭,立即扫码关注,获取更多软件动态和资源福利。
读者也喜欢这些内容:
-
如何将问卷星中的数据导入SPSS 如何对问卷星的数据进行SPSS分析
如今无论是在职场还是大学校园,都经常会用到问卷调查。问卷调查可以帮我们快速收集用户数据,了解用户的需求、关注点,帮助我们从数据中分析出研究方向、需要如何改进。而问卷星是常用的用来收集用户问题的问卷调查软件之一。下面就来说说如何将问卷星中的数据导入SPSS,如何对问卷星的数据进行SPSS分析的相关内容。...
阅读全文 >
-
SPSS显著性小于0.001的意义 SPSS显著性大于0.05怎么办
在使用SPSS软件进行数据分析工作的过程中,得到的显著性水平分析结果具有极为重要的作用。它能够帮助我们衡量变量之间是否存在真实的关联,或者不同组别数据之间是否存在实质性的差异。今天我们就一起来探讨关于SPSS显著性小于0.001的意义,SPSS显著性大于0.05怎么办的问题。...
阅读全文 >
-
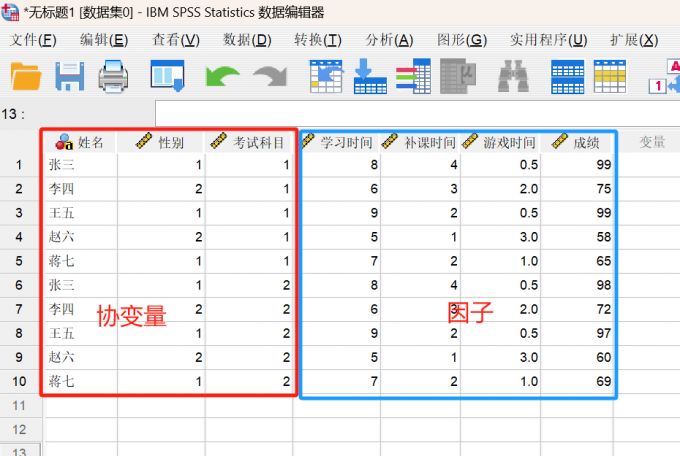
SPSS因子和协变量的区别和联系 SPSS因子和协变量怎么选
在SPSS数据统计分析方法中,回归分析是比较常用到的数据分析方法,其中多元 Logistic 回归分析是较为复杂的一种分析方法,因为其中包含了因子、协变量、因变量、自变量等多个变量,在进行分析的时候,需要区分好这些变量,接下来重点给大家讲解,SPSS因子和协变量的区别和联系,SPSS因子和协变量怎么选。...
阅读全文 >
-
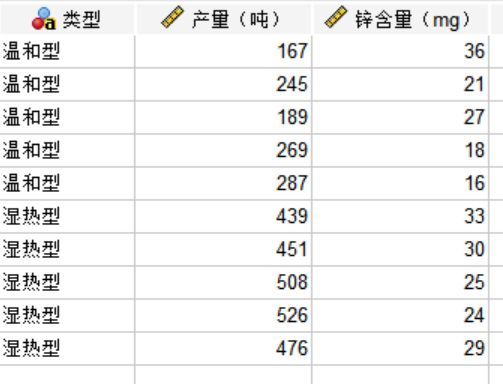
SPSS协变量是什么 SPSS协变量是控制变量吗
在数据收集阶段,当采集的数据繁杂众多,我们可以使用SPSS协变量分析来测算影响重要结果的潜在因素,减少某些变量对实验数据的干扰,由此准确识别多类变量之间的因果关系。今天,我们以SPSS协变量是什么,SPSS协变量是控制变量吗这两个问题为例,带大家了解一下SPSS协变量的相关知识。...
阅读全文 >




