

- 首页
- 产品
- 下载
-
帮助中心
SPSS回归分析贝塔值怎么看 SPSS回归分析贝塔值怎么求
发布时间:2022-07-11 11: 23: 14
品牌型号:Dell N5010
系统:Windows 10
软件版本:IBM SPSS Statistics试用版
Beta是指标准化系数,在多元线性回归分析中,未标准化系数不能指出哪些变量对因变量的影响程度大,标准化处理以后,可以用Beta系数分析自变量对因变量的影响程度,借助专业的统计分析软件IBM SPSS Statistics,我们可以非常简便的完成多元线性回归分析,并求解Beta值,SPSS回归分析贝塔值怎么看,SPSS回归分析贝塔值怎么求,本文将向大家作简单介绍。
一、SPSS回归分析贝塔值怎么看
进行多元线性回归分析时,查看拟合方程的系数不能确定哪些自变量对因变量的影响大,如果对系数进行标准化,标准化系数就能反映因变量的影响程度,标准化系数(Beta)公式如图1:
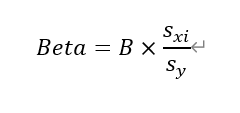
标准化系数计算公式 标准化回归系数=未标准化回归系数×该自变量的标准差/因变量的标准差。
Beta系数越大代表该变量对因变量影响越大,如图2中,VAR00001系数大于VAR00003系数,大于VAR00002系数,变量VAR00001对因变量影响最大,VAR00003次之,VAR00002最小。
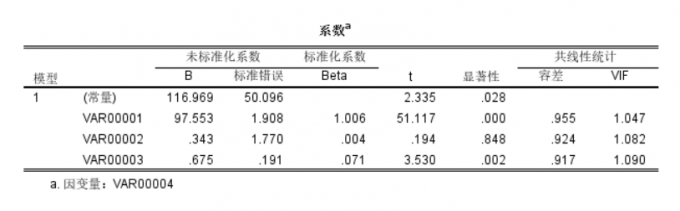
Beta系数表 我们可以查看一下原始数据,如图3所示。虽然VAR00001数值整体最小,但对因变量影响最大。
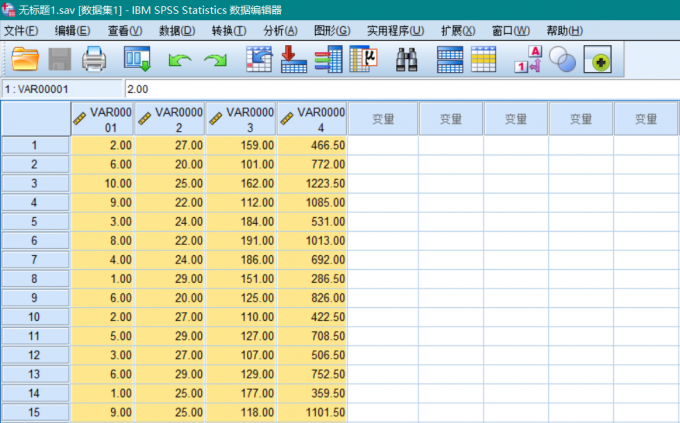
原始数据图 本小节介绍了贝塔值怎么看,下面向大家介绍贝塔值的求解方法。
二、SPSS回归分析贝塔值怎么求
仍然是图3中数据,点击分析,回归,线性,进入多元线性回归分析界面,如图4所示。
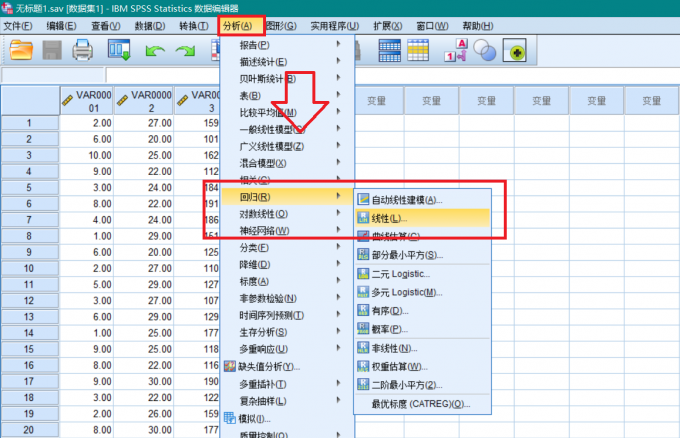
进入多元线性回归分析界面 在图5所示界面,将VAR00004加入因变量,将VAR00001,VAR00002 VAR00003 加入自变量,然后点击统计,勾选共线性诊断,点击继续,确定,SPSS将进行多元线性回归分析,并输出结果,结果中包含Beta系数。
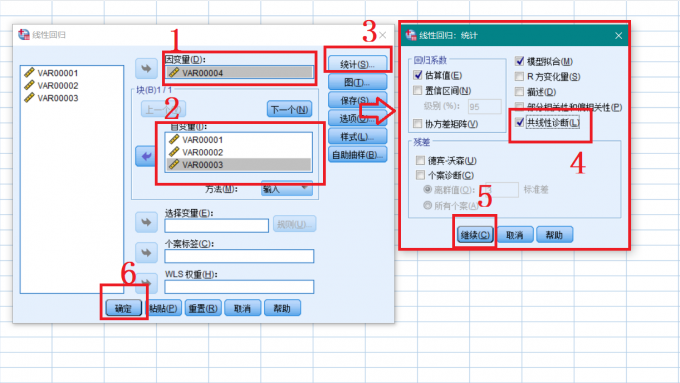
进行多元线性回归分析 进行共线性诊断是非常重要的,可以找出自变量中线性相关的数据,否则进行多元线性回归分析是没有意义的。我们在下一小节中继续介绍多元线性回归分析的结果解读。
三、SPSS多元线性回归分析结果解读
首先我们应该关注F值和共线性VIF值,这二者可以反映进行的多元线性回归分析是否有统计学意义,是否有效。
首先ANOVA表中,F值为609.292,显著性为0,小于0.05,说明分析结果有统计学意义,共线性VIF值均小于10,说明不存在共线性问题,回归分析有效。
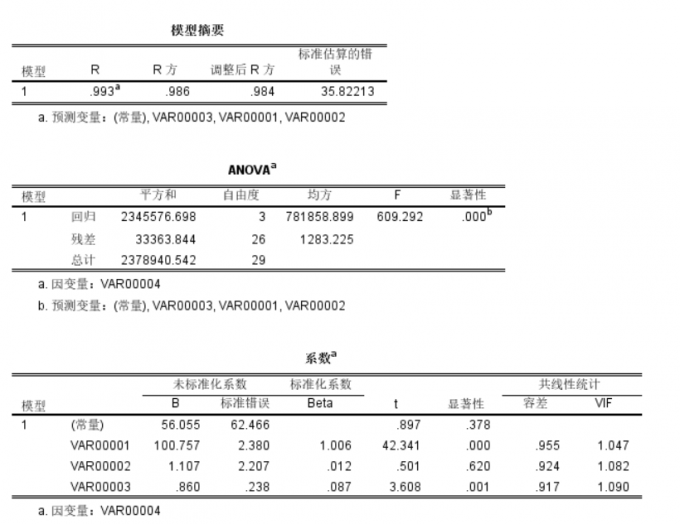
多元线性回归分析结果 然后我们查看系数表中的B列,得出未标准化的回归方程:
VAR00004=100.757* VAR00001+1.107* VAR00002+0.860* VAR00003+56.055
根据标准化系数Beta,可以得出VAR00001对因变量影响最大,VAR00003次之,VAR00002最小。该模型R值0.993,R越接近1,线性相关水平越高。
本文向大家介绍了SPSS回归分析贝塔值怎么看,SPSS回归分析贝塔值怎么求,以及回归分析结果怎么解读,在多元线性回归分析过程中,还应注意剔除偏离数据,注意线性回归系数t检验的显著性,限于篇幅,本文的实例未进行介绍,更多的内容大家可以登录SPSS中文网站查找学习。
作者:莱阳黎曼
展开阅读全文
︾
标签:SPSS,IBM SPSS Statistics,SPSS教程,回归分析,二元回归分析
读者也访问过这里:热门文章SPSS数据分析显著性差异分析步骤 SPSS显著性差异分析结果怎么看数据的显著性差异分析主要有三种方法,分别是卡方检验、T检验和方差分析。这三种方法都有具体的数据要求:卡方检验是对多个类别的数据进行分析,T检验是对两组数据进行分析,方差分析是对多组数据进行检验。下面,小编具体说明一下SPSS数据分析显著性差异分析步骤,SPSS显著性差异分析结果怎么看。2022-01-07实践SPSS单因素方差分析之检验结果解读在《实践SPSS单因素方差分析之变量与检验方法设置》一文中,我们已经详细地演示了IBM SPSS Statistics单因素方差分析方法的变量选择以及相关的选项、对比设置。2021-01-11spss如何做显著性分析 spss显著性差异分析怎么标abc在统计分析中,显著性分析是分析相关因素之间是否存在显著影响关系的关键性指标,通过它可以说明分析结论是否由抽样误差引起还是实际相关的,可论证分析结果的准确性。下面大家一起来看看用spss如何做显著性分析,spss显著性差异分析怎么标abc。2022-03-14SPSS回归分析中的f值是什么 SPSS回归分析F值在什么范围合适回归分析中以R表示相关性程度的高低,以F评价回归分析是否有统计学的意义,使用IBM SPSS Statistics进行回归分析,可以非常快速的完成R,F的计算,并且给出回归曲线方程,那么,SPSS回归分析中f值是什么?SPSS回归分析F值在什么范围合适,本文结合实例向大家作简单的说明。2022-07-22SPSS多元logistic回归分析的使用技巧回归分析是数据处理中较为常用的一类方法,它可以找出数据变量之间的未知关系,得到较为符合变量关系的数学表达式,以帮助用户完成数据分析。2021-04-26SPSS相关性分析结果怎么看相关性分析是对变量或个案之间相关度的测量,在SPSS中可以选择三种方法来进行相关性分析:双变量、偏相关和距离。2021-04-23最新文章SPSS随机值检验步骤 SPSS随机检验结果怎么看很多人都听过IBM SPSS Statistics这款软件,它是数据分析的可靠搭档,不仅能轻松搞定数据的整理、转换,最后还能自动生成图表,对新手非常友好。对于经常需要进行学术研究、市场调研的用户来说是个常用的选择。今天我们就来说一下SPSS随机值检验步骤,SPSS随机检验结果怎么看的相关内容。2026-01-30SPSS为什么没有事后检验 SPSS事后检验结果怎么看SPSS作为一款优秀的数据统计分析软件,深受数据统计分析人员的喜爱。SPSS之所以这么受欢迎,除了SPSS有很多的数据统计分析方法,可以帮助统计分析人员更高效的进行数据分析,还因为SPSS的人性化操作,一些刚入行的统计小白,也可以快速的掌握SPSS,接下来给大家详细介绍有关SPSS为什么没有事后检验,SPSS事后检验结果怎么看的相关内容。2026-01-30SPSS重复测量怎样分析 SPSS重复测量球形性应如何检验重复测量是数据分析中的一个重要环节。主要用来分析和检验数据样本中同一对象的相同指标在不同条件或者环境之下的变化情况,所以需要对这部分数据进行重复的测量和分析。例如我们统计一组大学生毕业后的就业情况,那么大学生的专业分类和性别都一致的情况下,就需要分析不同的就业影响因素对于最后就业率的影响。下面给大家介绍SPSS重复测量应当怎样分析,SPSS重复测量球形性应如何检验。2026-01-14SPSS亚组分析的注意事项 SPSS亚组分析结果解读对于经常与数据分析打交道的小伙伴来说,想必对亚组分析这个概念应该不会感到陌生。亚组分析是用来检测异质性结果的方法之一,亚组分析的数据结果分为确证性、支持性和探索性三类。而我们在进行亚组分析时,可以借助数据分析软件SPSS的帮助,它一方面可以帮助我们得到亚组分析的数据结果,还能够把这些数据分析结果以报告形成呈现出来。接下来给大家介绍SPSS亚组分析的注意事项, SPSS亚组分析结果解读的具体内容。2026-01-14SPSS卡方检验样本不满足要求怎么办 卡方检验SPSS结果都小于0.5说明了什么在数据分析的过程中,卡方样本检验是常见的一种统计方式。卡方检验主要用来检验数据样本之间的离散程度,进而判断不同数据之间的偏差值,如果数据样本在统计的时候不符合实际的统计需求,就可能导致卡方检验不满足要求。所以我们需要在统计的过程中对数据样本和统计方法进行调整,这样能够规避数据样本检验带来的结果偏差风险。下面以SPSS为例,给大家介绍SPSS卡方检验样本不满足要求怎么办,卡方检验SPSS结果都小于0.5说明了什么的具体内容。2026-01-14SPSS事后比较怎样进行 SPSS事后比较多重校正应如何设置在数据分析的过程中,经常会在数据分析之后对它进行事后比较的操作。事后比较可以在方差分析的基础之上帮助我们快速找到具体存在差异的数据组。简单来说,大家可以把方差分析理解为起到了一个提示作用,告诉了我们数据样本中的均值并不相等且存在差异,但是如果想要找到具体的差异点在哪里,就需要用到事后比较了。而在进行事后比较的过程中,还会遇到设置多重校正的情况。下面以SPSS为例,给大家介绍SPSS事后比较怎样进行,SPSS事后比较多重校正应如何设置。2026-01-14微信公众号
欢迎加入 SPSS 产品的大家庭,立即扫码关注,获取更多软件动态和资源福利。
读者也喜欢这些内容:
-
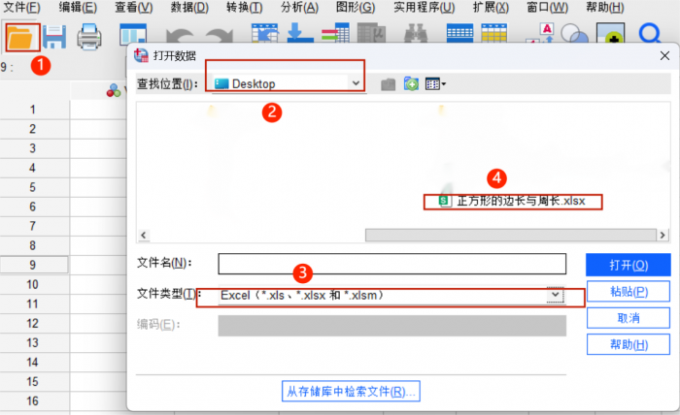
SPSS可以打开Dta文件吗 SPSS可以画图吗
探究生物基因排列的规律、调查社会思潮的主流、掌控消费流行的趋势,数据分析深入到了我们生活的每个角落,SPSS就是能够帮助我们进行高效、精准数据分析的软件。SPSS是兼容性很高的数据分析软件,但是并不适合所有的文件格式。接下来我就在介绍SPSS可以打开Dta文件吗,SPSS可以画图吗等问题的基础上,具体介绍一下这款软件。...
阅读全文 >
-
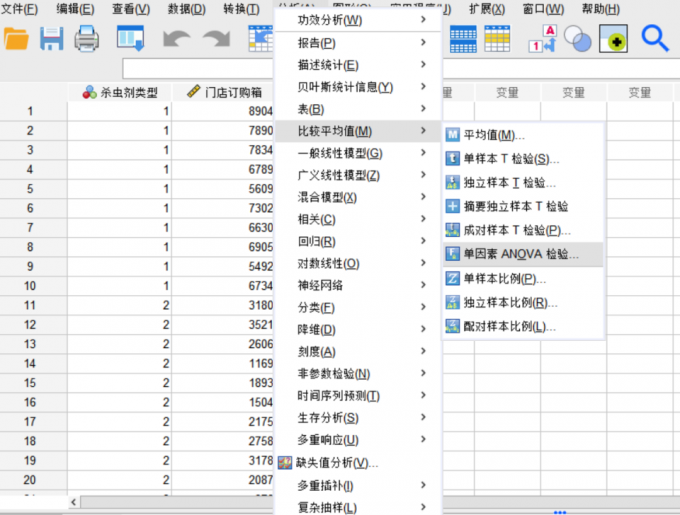
SPSS Tukey检验是什么 SPSS Tukey检验怎么做
在数据分析领域,Tukey事后检验经常作为SPSS方差分析的重要结果,也就是被用来分析多组变量在某方面的水平均值是否具有显著差异,例如不同类型药物的治疗效果、不同款式产品的销售量、不同年龄段儿童的智力发育水平等等。本文以SPSS Tukey检验是什么,SPSS Tukey检验怎么做这两个问题为例,简单介绍一下Tukey检验的相关知识。...
阅读全文 >
-
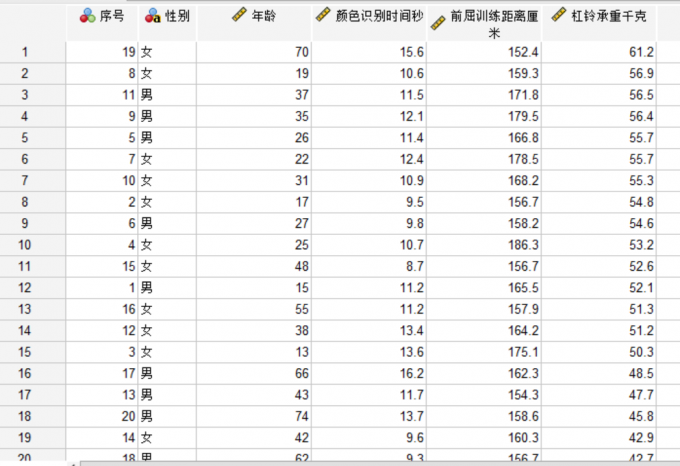
SPSS数据转置什么意思 SPSS数据转置怎么操作
在进行SPSS数据计算和分析之前,研究者通常运用SPSS数据转置的方法,借此对繁杂数据进行行列互换,适用于EXCEL、CSV、文本数据、SAS等各类形式的数据文本,便于研究者清晰全面地了解数据信息。本文以SPSS数据转置什么意思,SPSS数据转置怎么操作这两个问题为例,带大家了解一下SPSS数据转置的相关知识。...
阅读全文 >
-
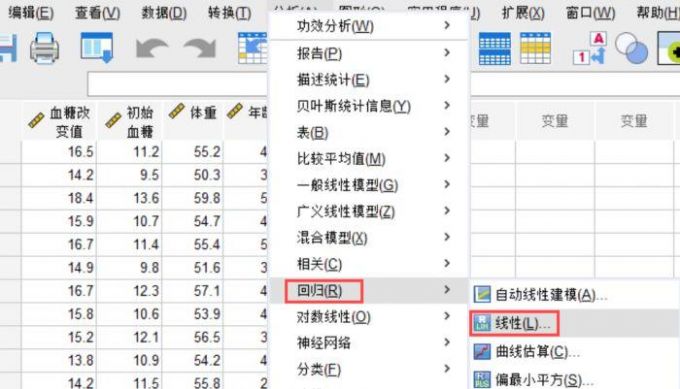
SPSS标准化残差图怎么做 SPSS标准化残差图解读
在数据分析领域,如果研究者想对线性数据集的正态性进行分析,推荐使用SPSS残差图绘制的方法来高效掌握采集的数据信息,以便了解数据模型的拟合情况和误差分布。今天,我们以SPSS标准化残差图怎么做,SPSS标准化残差图解读这两个问题为例,带大家了解一下SPSS标准化残差的相关知识。...
阅读全文 >
-